Waves in a Julia set on the Riemann sphere
film
Lizenz
Autoren
- Nils Berglund
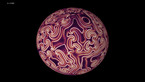
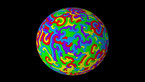
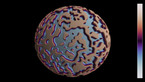
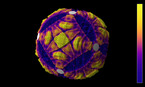
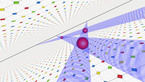
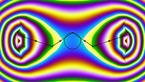
A solution of the wave equation in a domain on the Riemann sphere, which is given by an approximation of a Julia set with parameter 0.37468 + 0.21115 i. The initial state is given by two circular waves, with opposite longitudes and positive latitude, and opposite sign.
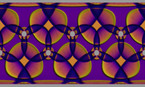
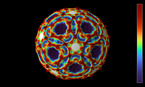
Finite difference simulation of the wave equation on a sphere. There are Dirichlet boundary conditions on a discrete approximation of a Julia set, that has been scaled and then projected stereographically on a Riemann sphere, with the origin mapped to the north pole of the sphere. There are some artifacts at the north pole, due to the singularty of spherical coordinates.
In part 1, the colors and radial coordinate show the wave height. In part 2, they show the energy averaged over a time interval. The point of view rotates around the sphere in the course of the simulation.