The Allen-Cahn equation on the two-dimensional torus
film
Lizenz
Autoren
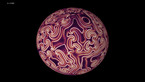
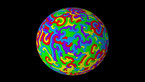
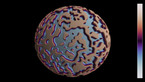
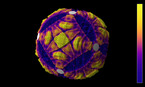
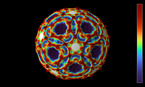
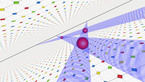
This is a 3D rendering of a solution of the Allen-Cahn equation in a rectangular domain with periodic boundary conditions. Both the z-coordinate and the color hue show the value of the solution, with blue indicating positive values, and red indicating negative ones. By increasing the viscosity (which measures the magnitude of diffusion) over time, one accelerates the coarse-graining dynamics of the system, separating blue and red phases. The luminosity depends on the angle between a normal vector to the surface and a fixed direction, to emulate the effect of a far away light source.
The Allen-Cahn equation models systems showing phase separation, such as ferromagnets with positively and negatively magnetized domains. These appear as red and blue areas in the simulation, while purple areas are those without magnetization. The Allen-Cahn equation is a nonlinear variant of the heat equation. Like the heat equation, it features a term that tends to make the field constant, given by a Laplace operator performing a local average around any given point, and pushing this average towards zero. Unlike for the heat equation, however, there is another term in the equation pushing the field towards 1 if it is positive (shown here in blue), and towards -1 if it is negative (shown here in red).
Render time: 45 minutes 30 seconds
Color scheme: Twilight by Bastian Bechtold https://github.com/bastibe/twilight
Music: “Sunrise in Paris” by Dan Henig
The simulation solves the Allen-Cahn equation by discretization.
C code: https://github.com/nilsberglund-orleans/YouTube-simulations