In Plato’s original text about the regular polyhedra, shapes of the four elements, fire, water, earth and air, the dodecahedron, as fifth element, — usually denoted as symbol for the world itself — is not mentioned.

‘eti de ousês sustaseôs mias pemptês, epi to pan ho theos autêi katechrêsato ekeino diazôgraphôn.’

(Plato, Timaeus 55C).

Several authors in history (cf. Cornford, Taylor, Heath) are arguing about this phrase in Plato’s description of the composition of triangles to form the well-known regular solids in Theaetetos’  dialogue: It starts with tetetrahedron, the octahedron, and the icosahedron and ends with the cube. He does not mention the dodecahedron. Plato himself added instead the above obscure remark about the fifth element, translated as:  

 ’Since there is another fifth configuration the demiurge uses it for the delineation of the universe. ’ (Plato, Timaeus, 55C).

     The possible solution of Plato’s riddle about the fifth element is the golden heptahedron,

named epitahedron (Quehenberger, 2014). It is the 3D representation of the Penrose Kites and Dart tiles

(Penrose, 1974). The Penrose patterns are irregular tilings of the plane in the proportion

of the golden ratio and are considered as a 2-dimensional slice of the 5-dimensional space.

Hence, the epitahedron, its 3-dimensional form constructed from the triangles of the

Robinson decomposition, is a unit-cell of higher dimensional space configurations.

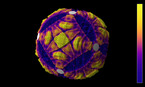
Epitahedra (E±) exist in two shapes: the concave E- (‚E minus’) is depicted on the top

and the convex E+ (‚E plus’).  

These manifolds composed of four golden triangles with edges in the length 1, 1, PHI

 and four golden triangles with edges in the length PHI , PHI , 1 which can be assembled into two golden tetrahedra. The volumes

of the epitahedra, both together (EE) and the concave (E-) to the convex (E+) –  are conform to the golden ratio: E- : E+ = E+ :

EE . Thus the epitahedron tiles space in the golden ratio analogous to the Penrose Tiling of the 2D plane.

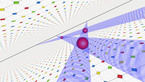
The movie shows the icosahedron filled with five epitahedra and the intersection of two epitahedra forming a dodecahedron in the

center.

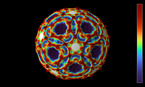
The last picture shows a 4-dimensional dodecahedron created by twelve epitahedra. According to this, the 5th element constitutes

Plato’s geometrical matrix in the formation of the physical universe, which still holds in terms of group theoretical descriptions  of

particles.

In this sense, Plato’s ontologic concept of triangles cradled by the wet-nurse of becoming turns out to be valid after 2400 years.