The film Epita-Dodecahedron will be screened in the program
Austrian Animated Experiments - 30 Years ASIFA AUSTRIA
at the kinoteka.
October 30, 2015 Ljubljana, (Slovenia)
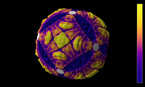
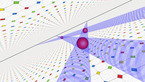
The epita-dodecahedron visualizing Poincaré's dodecahedral space
película
Licencia
Créditos
- Renate Quehenberger
Analogous to Henri Poincaré’s concept of dodecahedral space the epita_dodecahedron allows to visualize the principle of the counter-movements of the opposite polyhedra E+ instead of the pentagonal spaces in his description of the homology sphere in the fifth “Complément” : Thus it clearly shows the different evolving symmetries,- crystallizing in steps of 36 degrees, just as Poincaré anticipated the shape of the universe in 1904.
The epitahedron, a newly discovered heptahedron, is assigned as the 3-dimensional representation of the Penrose kites and darts. The lengths of the edges as well as the volumes of the epitahedra – E- (concave) E+ (convex) and both together, EE (E- : E+ = E+ : EE ) – are conform to the golden ratio. φ (≅ 1.618). Thus epitahedra are tiling the space in the golden ratio analogous to the irregular Penrose Tiling in the plane, which is a slice of the 5-dimensional space.
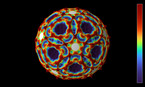
By composing 12 epitahedra to a dodecahedron,- which is named epita-dodecahedron, naturally another dodecahedron within a complex intersecting space configuration appears in the center. This is connected to the fact, that epitahedra can be enfolded from one single pentagon, although this way one obtuse triangle is missing (Quantum Cinema, 2012). So it can be regarded as a 3-dimensional pentagon which makes evident that their composition must result in higher dimensional configurations. The intersection of the apices of the 12 polyhedra basically form 25 subspaces with various shapes in the center due to the stellating effect of their 60 faces.This are the quantum mechanically important 26 dimensions. In the center of the epita-dodecahedron, another small dodecahedron appears within a complex intersecting space configuration. So far, we have been able to identify four different central solids: a dodecahedron, the icosahedron, and the icosidodecahedron belonging to the group of Archimedean solids and a (thus far unmentioned) stellated icosidodecahedron. The pentagonal pyramid cells, which sit on each face of the dodecahedron are giving rise to the small stellated dodecahedron.
The dodecahedral space based on Poincaré’s idea was first given by Threfall and Seifert who characterized by the use of a dodecahedron the opposite faces of which are identified after a turn by π/5. It is called spherical because it is bounded by spherical pentagons due to the fact that it is obtained as the intersection of 12 balls. (Threlfall & Seifert,1931)
Analogous to this concept the epita_dodecahedron allows to visualize the principle of the described counter-movements of the opposite polyhedra E+ instead of the pentagonal spaces in Poincaré‘s description of the homology sphere in the fifth “Complément” : Thus it clearly shows the different evolving symmetries,- crystallizing in steps of 36 degrees, just as Hernri Poincaré anticipated in 1904. (Poincaré,1904)
Thus this unit cell of the higher dimensional space enables the composition of an infinitely inflatable space that has the boundary in the shape of a dodecahedron; similar to the boundary of the Penrose Pattern, a pentagon of decagonal shape analogous to the symmetry axis. The art-science author Arthur I. Miller summarizes it as follows:
The fifth element - the quintessence has its geometrical form as epitahedron and we live in a Poincaré dodecahedral space, after the french polymath Henri Poincaré. (Miller, 2013)