Transition from 3-branched to 5-branched spirals in the Rock-Paper-Scissors-Lizard-Spock equation
película
Licencia
Créditos
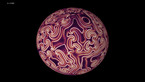
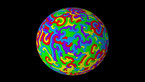
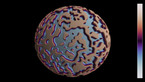
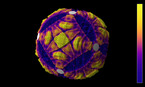
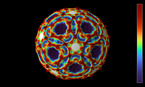
Solution of a reaction-diffusion equation involving five chemicals, each of them dominating two others. There are two interaction parameters, which are equal at the beginning of the simulation. As one of them decreases to zero, spirals with 5 branches appear.
The game Rock-Paper-Scissors-Lizard-Spock was originally created by Sam Kass with Karen Bryla for the sitcom Big Bang theory (see https://youtu.be/x5Q6-wMx-K8 ). It is a variant of the Rock-Paper-Scissors game, in which each of the five words beats two others, and is beaten by the two other ones:
- Rock (red) beats Scissors and Lizard, and is beaten by Paper and Spock
- Paper (yellow) beats Rock and Spock, and is beaten by Scissors and Lizard
- Scissors (green) beat Paper and Lizard, and are beaten by Rock and Spock
- Spock (blue) beats Scissors and Rock, and is beaten by Lizard and Paper
- Lizard (purple) beats Spock and Paper, and is beaten by Rock and Scissors
This simulation shows a solution of a reaction-diffusion equation that imitates the game. There are five chemicals, which diffuse, and transform into each other. Each chemical can convert two other ones into its own type, while it is converted by the other two.
In this version, the 10 possible interactions are grouped into 2 families of 5 interactions each, with different coupling constants. One of them is kept constant, while the other one decreases in the course of the simulation.