MathLapse - Monge's Theorem
película
Licencia
Créditos
- Video and animation
- Music
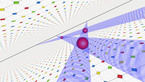
The Monge’s Circle Theorem as a silhouette of a higher dimension
The Monge’s Circle Theorem states that for any three circles, none of which is completely inside another, the intersection points of the common external tangents are colinear. Let’s try to make this theorem intuitivelly obvious.
Imagine this:
- three spheres with equal sizes, but at different distances from us
- the pairs of spheres are neatly placed in infinitely long tubes
- the tubes converge into points somewhere on the horizon.
Our intuition says that the horizon is only one. Whatever direction the tubes go, they will always vanish into that same horizon.
Now, forget all about colours and shadings. Look only at the silhouettes. The three spheres become the three circles. The outlines of the three tubes are the external tangents. And the horizon … is the line where all tubes-tangents vanish into points.
Could you find another theorem, which could be interpreted as a silhouette of a higher dimension?