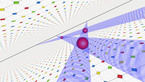
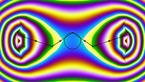
Spirals in the rock-paper-scissors equation on the sphere
película
Licencia
Créditos
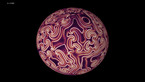
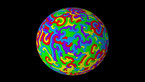
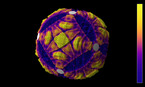
Solution of a reaction-diffusion equation involving three chemicals, each of them dominating one of the others, and dominated by the other one.
At each point in space and time, there are three concentrations u, v, and w of chemicals, that we may call Red, Blue and Green. Denoting by rho = u + v + w the total concentration, the system of equations is given by
d_t u = D*Delta(u) + u*(1 - rho - a*v)
d_t v = D*Delta(v) + v*(1 - rho - a*w)
d_t w = D*Delta(w) + w*(1 - rho - a*u)
where Delta denotes the Laplace operator, which performs a local average, and the parameter a is equal here to 0.75 while D is equal to 0.2. The terms proportional to a*v, a*w and a*u denote reaction terms, in which Red is beaten by Blue, Blue is beaten be Green, and Green is beaten by Red. The situation is thus similar to the Rock-Paper-Scissors game, and there exist simpler cellular automata with similar properties,The equation is solved by finite differences, where the Laplacian is computed in spherical coordinates. Some smoothing has been used at the poles, where the Laplacian becomes singular in these coordinates.
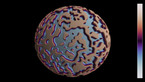
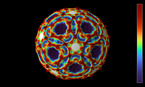
To obtain the vorticity, the values of u, v and w are first converted into an angle with the following steps:
- divide u and v by the total density rho = u + v + w
- set x = (u - 1/3) + (v - 1/3)/2 and y = (v - 1/3)*sqrt(3)/2
- convert (x,y) to polar coordinates
The resulting transformation from (u,v,w) to (x,y) is similar to a discrete Fourier transform with 3 modes. The color hue depends on the resulting angle, and the radial coordinate depends on its spatial gradient.