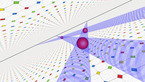
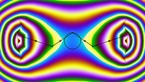
The film Epita-Dodecahedron will be screened in the program
Austrian Animated Experiments - 30 Years ASIFA AUSTRIA at the
Animated Dreams, 17th international Animation Film Festival, Tallinn (Estonia)
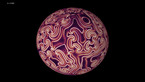
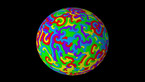
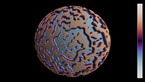
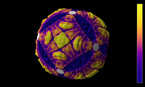
The epita-dodecahedron visualizing Poincaré's dodecahedral space
영상
저작권
크레딧
- Renate Quehenberger
앙리 푸앵카레(Henri Poincare)가 그의 책 “Complément” 에 사용된 오각형 공간의 역방향 운동을 정십이면체 공간을 이용해 시각화했듯이, 에피타 정십이면체(Epita-dodecahedron)는 이와 반대되는 다면체인 E+의 역방향 운동을 시각화해줍니다. 이는 푸앵카레가 1904년 예측했던 우주의 모양을 보여줍니다.
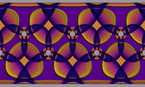
최근 새롭게 발견된 칠면체인 에피타히드론(Epitahedron)은, 펜로즈(Penrose)정방체와 다트의 3차원적 표현입니다. Epitahedra E- (오목버전), Epitahedra E+ (볼록버전), 그리고 둘 다 합친 Epitahedra EE의 모서리들의 길이와 부피들은 모두 황금비(the Golden Ratio φ ≅ 1.618)를 품고 있습니다. 그렇기에 3차원 공간에서의 Epitahedra 타일링은 2차원 평면에서의 펜로즈 타일링(Penrose Tiling)의 3차원 버젼입니다.
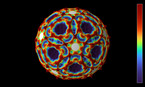
에피타 정십이면체(Epita-dodecahedron)는 Epitahedra를 12개 모아 만든 물체로, 자연스레 이 중심에는 또 다른 정십이면체가 만들어지게 됩니다. 왜냐하면 Epitahedra가 하나의 오각형으로부터 접어질 수 있기 때문입니다. 그러므로 Epitahedra는 3차원 버젼의 오각형으로 생각될 수 있으며, 이들의 집합체는 그보다 더 높은 차원 위에 존재해야 함을 알 수 있습니다. 12개의 Epitahedra가 겹치면서 만드는 공간은 그 중심에서 25가지 다양한 모양의 하위 공간을 만들게 됩니다. 이들이 양자역학에서 중요한 26차원을 구성합니다. 에피타 정십이면체의 중심에선 또 다른 작은 정십이면체가 발견됩니다. 현재 우리는 이 중심에서 4가지 다른 정다면체들을 발견하였습니다.
푸앵카레가 생각해넨 정십이면체 공간은 1931년 Threfall 과 Seifert라는 사람들이 처음 만들어냈습니다. 이들의 방법과 유사한 방식으로, 에피타 정십이면체(Epita-dodecahedron)는 이와 반대되는 다면체인 E+의 역방향 운동을 시각화해줍니다. 이는 푸앵카레가 1904년 예측했던 우주의 모양을 보여줍니다.