Waves with octahedral symmetry on the sphere
영상
저작권
크레딧
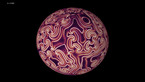
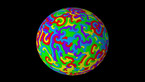
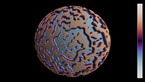
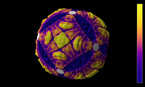
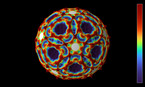
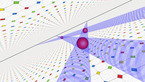
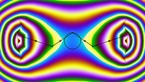
Solution of the wave equation on a sphere. Reflecting obstacles have been placed around the vertices of a regular octahedron. The initial state is a set of circular waves concentrated at the centers of the faces of the octahedron. The colors and radial coordinate represent the wave height and averaged wave energy.
he simulation shows a solution of the wave equation on a sphere, obtained by a finite difference scheme. There are Dirichlet boundary conditions on a set of discs of constant radius placed on the vertices of a regular octahedron. The initial state is a set of circular waves concentrated near the centers of the faces of the octahedron, which form a cube.
Part 1 shows the wave height, and part 2 shows the wave energy, averaged from the beginning of the simulation.