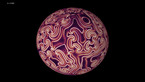
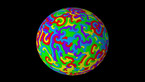
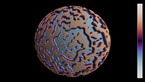
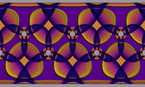
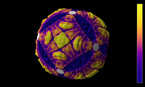
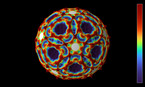
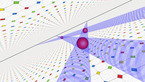
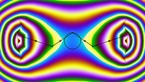
Waves in a Julia set on the Riemann sphere, 2d projection
영상
저작권
크레딧
A solution of the wave equation in a domain on the Riemann sphere, which is given by an approximation of a Julia set with parameter 0.37468 + 0.21115 i. The initial state is given by two circular waves, with opposite longitudes and positive latitude, and opposite sign. The video shows an equirectangular projection of the sphere.
Finite difference simulation of the wave equation on a sphere. There are Dirichlet boundary conditions on a discrete approximation of a Julia set, that has been scaled and then projected stereographically on a Riemann sphere, with the origin mapped to the north pole of the sphere. The result is then mapped to a rectangle by an equirectangular projection, in which the x- and y-ccordinate are proportional to longitude and latitude, respectively.
In part 1, the colors and radial coordinate show the wave height. In part 2, they show the energy averaged over a time interval. The point of view rotates around the sphere in the course of the simulation.