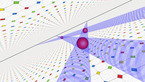
Allen-Cahn equation on the sphere
films
Licence
Crédits
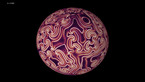
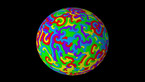
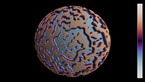
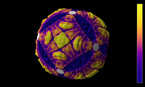
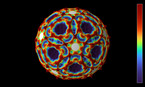
3D render of the Allen-Cahn equation on the 2-sphere. The color hue and radial coordinate indicate the value of the field, with red corresponding to positive values, and blue to negative values.
The Allen-Cahn equation models systems showing phase separation, such as ferromagnets with positively and negatively magnetized domains. These appear as red and blue areas in the simulation, while purple areas are those without magnetization. The Allen-Cahn equation is a nonlinear variant of the heat equation. Like the heat equation, it features a term that tends to make the field constant, given by a Laplace operator performing a local average around any given point, and pushing this average towards zero. Unlike for the heat equation, however, there is another term in the equation pushing the field towards 1 if it is positive (shown here in red), and towards -1 if it is negative (shown here in blue).
Render time: 41 minutes 2 seconds
Color scheme: Twilight by Bastian Bechtold https://github.com/bastibe/twilight
Music: “Ether” by Text Me Records / Bobby Renz
The simulation solves the Allen-Cahn equation by discretization.
C code: https://github.com/nilsberglund-orleans/YouTube-simulations