The Penrose-Riemann Connection
films
Licence
Crédits
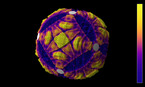
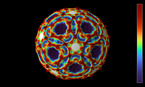
The film is about discretization of patterns, colours and shapes. The animation illustrates that a 2D periodic pattern can be mapped seemless to a torus. Riemann surfaces are more suitable to display aperiodic patterns in three dimensions. Hence the Penrose tiling consisting of birds is shown on a helicoid.
The very beginning is a “big bang” - where a single point expands. There can be seen the genesis of a periodic sea life pattern in the plane. The pattern transforms to a solid with hexagonal profile. The prism is bent to a ring, and the grade of approximation increases. The torus is morphed to a catenoid. The sea life motif suddenly shows a singularity (Droste effect).
The second part shows special properties of Penrose tilings. Every part of the pattern repeats endlessly, but there exists no translation to make the pattern fit as a whole. The discretization of the bird motives reveals hidden structures. The Penrose tiling is used to illustrate Moiré effects and refinements. The Riemann surface acts out as helicoid. The mapped aperiodic tiling leads to a seemless representation in three dimensions. The animation ends with the message to use mathematics to make the world a better place.
The software VaryLab from SFB TRR 109 - Discretization in Geometry and Dynamics – was used to map geometric patterns to objects without linear distortion.