MathLapse – Cybernetic Self-Similarity
films
Licence
Crédits
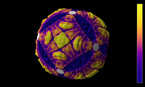
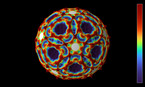
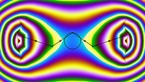
The video shows a polygonal line consisting of 24 segments constructed by turtle geometry (Refs.: “Turtle Geometry” by Harold Abelson and Andrea diSessa, The MIT Press, 1982).
The angle between segments is linearly incremented segment by segment. The angle increment of the initial figure at video start is 15 degrees. I. e. the angle between first and second line is 15 degrees, the angle between second and third line is 30 degrees, the angle between third and fourth line is 45 degrees etc. This construction rule leads to a symmetric figure. When starting the video, the angle increment increases with time leading to a “dancing” figure changing its shape continuously. As a quite fascinating effect, parts of the figure become similar to other parts overlapping each other (a special kind of self-similarity?!). At the time 3:10 and 6:51 of the video, the figure degenerates even to a single line. After a while, the “dance” starts again with the initial figure and continues with the same complex periodic motion.