MathLapse - Spinning in various dimensions
영상
저작권
크레딧
In 2d we can spin a ray about a point. If the ray contains a 1d profile, spinning gives a 2d object.
In 3d we can spin a half plane about a line. If we the half plane contains a 2d profile, spinning gives a 3d object.
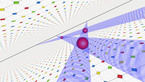
In 4d we can spin a half space about a plane. If the half space contains a 3d profile, spinning gives a 4d object.
This MathLapse demonstrates how we can get an object via spinning of an object of one dimension less. In particular, spinning a 3-dimensional arc we can get a 4-dimensional knot.
We start in dimension 2: we mark some points on a ray (blue) and spin the ray about its endpoint (white). We get a cd, which can be considered a 2d object.
In dimension 3 we mark some points in a half plane (blue) and spin the half plane about its boundary line (white). We get a vase, a 3d object.
We can visualize the spinning and the vase in 2d, assigning colors to the points of the vase according to their height, like in an elevation map.
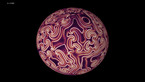
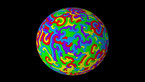
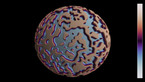
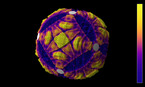
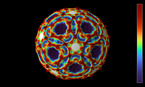
In dimension 4 we take an arc contained in a half space (blue) and spin the half space about its boundary plane (white). We can only visualize the process in 3d, but the colors encode the height in the fourth dimension. We get a 4d object, a knotted sphere!
This construction of 4d knots was proposed by the mathematician Emil Artin in a research paper in 1925.