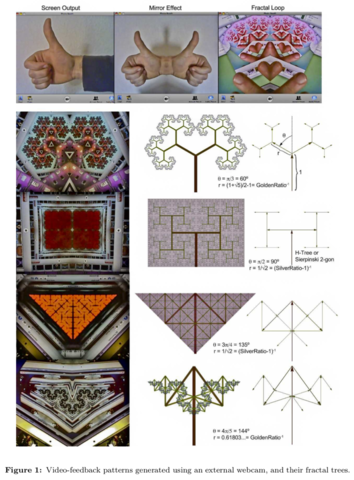
Video-feedback loop! Exploring mirror-symmetric binary complex trees
체험활동
저작권
크레딧
Plug a USB webcam, open an app like Photo Booth or Chrome’s Webcam Toy, enable the mirror effect, and then point your webcam to the screen. What do you see? The images get trap in a fractal attractor that you have just created by closing the video-feedback loop! The camera roll angle acts as the argument of the complex number and the distance from the camera to the screen acts as its modulus. Isn’t it wonderful? Have fun exploring this space of fractals that live in the complex plane.
One of the most spectacular and accessible phenomena related to the bilateral symmetry is the generation of video-feedback complex trees in a computer screen. If the screen has a mirror effect enabled*, and a webcam starts to record its own output, the system will run into a loop that traps, transforms and copies the recorded frames again and again until they are reduced to mere fixed points forming a fractal attractor. Changing the camera roll angle or the distance to the screen, different fractal patterns emerge. The attractors of this home-made dynamical system are analogous to a family of IFS fractals generated by a pair of affine transforms. The figure below compares four video-feedback attractors with their associated symmetric binary complex trees.
*Mac users can use the mirror effect available in the Photo Booth app. Windows and Linux users can achieve the same effect with a Chrome’s app called Webcam Toy.