The Heidelberg Laureate Forum Foundation invites you to visit the exhibition “Mathematics of Planet Earth” at Karlstorbahnhof in Heidelberg, Germany! It runs from July 5 to Aug 2, 2015, for the first time in Heidelberg. It offers a big variety of exciting adventures for children and adults alike.
Quasicrystalline Wickerwork
In 1982, Dan Shechtman discovered a nuclear structure with fivefold rotational symmetry. Today, nuclear structures of this type are called quasicrystals.
In general, growth models for decagonal quasicrystals with tenfold or fivefold rotational symmetry are based on geometric, quasiperiodic tilings which were found by Roger Penrose in 1973.
For the latest images, press the left arrow!

Quasicrystalline Wickerwork
Although the wickerwork in the foreground of the large graphic is composed of medieval girih tiles (Persian girih, Eng. knot), it has a relationship to the atomic structure of a decagonal quasicrystal.
Adapting the girih tiles to a modern rhombic Penrose tiling they are generating a girih wickerwork with a good approximation to a tenfold rotational symmetry. The resulting closed nodes (green, yellow and blue) surprisingly correspond to the geometry of a cover model commonly used today, which can be seen in the background of the wickerwork.
For a detailed description of the picture please refer to the pdf-documents (GERMAN/ENGLISH) provided below and to the files below the image.
This picture, like some others from this gallery, is part of the exhibition “IMAGINARY - Form und Formel mathematischer Fantasie” which was first shown in June 2016 in Nuremberg.
(www. imaginary.org/event/imaginary-in-nuremberg)
(www. imaginary.org/event/imaginary-at-sigena-gymnasium-in-nuremberg)
(www. imaginary.org/gallery/hand-made-hands-on)
(https://patterninislamicart.com/s/collections/main-archive/piia_image/tu…) Girih pattern in Kayseri
Woman Teaching Aperiodic Geometry
The underlaying structure of this image is a quasiperiodic (aperiodic) rhombic Penrose tiling, a geometric structure used for modeling decagonal quasicrystals.
The shape of the yellow colored area has a tenfold rotational symmetry although its center is dissymmetric. This array is commonly called cartwheel.
By taking up 35 different positions the young woman demonstrates what is meant by doing a cartwheel. As an allusion to the difficult order of a spatial rhombohedral Penrose tiling she turns 15 times her back on us.
Please compare chapter III of the Description Booklet (GERMAN/ENGLISH) provided below as pdf-document.
Hands-on objects that illustrate a growth algorithm (Quasiperiodic Succession, chapter V) with which a flawless cartwheel structure can be successively built can be found in the second half of the gallery Hand made hands-on.
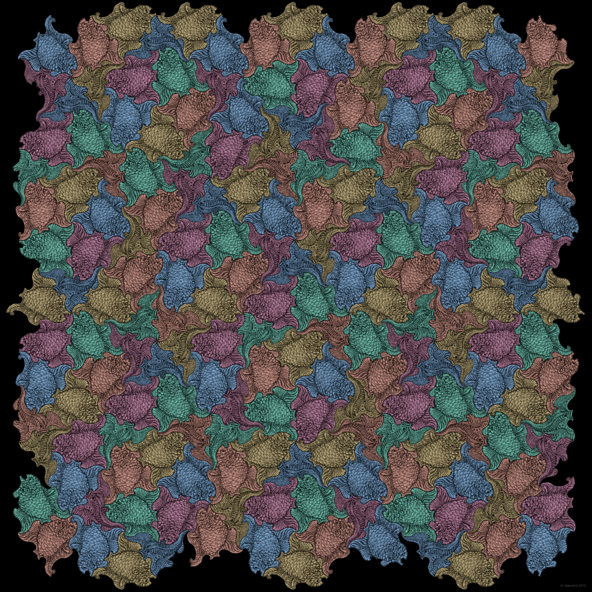
Animalistic Quasiperiodicity
The opposite image was inspired by the famous work of the well-known Netherlands artist M. C. Escher who joined his figures in a similar flawless way.
Escher’s principles of arrangement were periodic with a correspondance to the atomic order of crystals. In contrast, the image which is presented here is based on a quasiperiodic Penrose tiling and so it corresponds to a quasicrystalline atomic order with fivefold rotational symmetry which cannot be crystallographic.
The red colored fish swim in five different orientations which are rotated by 36 degree to one another.
The turquois coloring let us detect the shape of the hub of a cartwheel.
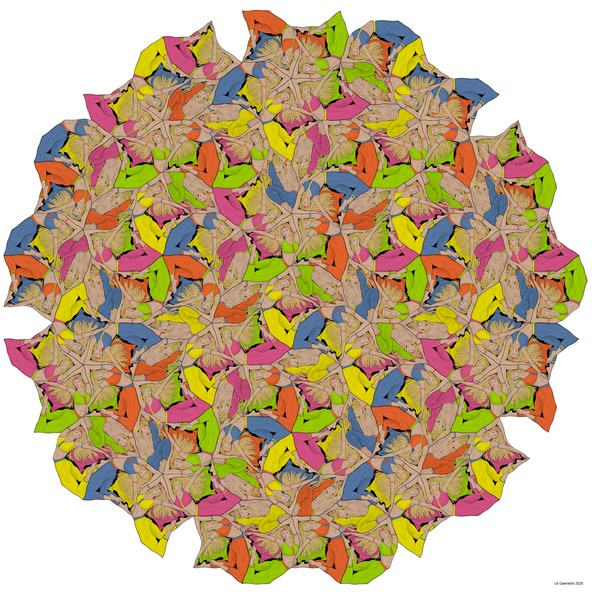
Animalistic Tiling Structure
This image shows the correspondence of the quasiperiodically ordered animals to four different but mutual derivable tilings.
The ring-shaped area is composed of yellow and orange triangles, called Robinson triangles. Inside the ring the triangles are combined to thick blue and small green Penrose rhombs, at its outside to blue kites and green darts.
All kites have a one-to-one correspondance to a blue, green or yellow pentagon of the Penrose pentagon tiling in the background. The concave corner of a dart is always in the center of a black pentagon, the arrowhead of a dart is in the center of a purple one. The white and black points represent the matching rules of the kite & dart tiling.
Animalistic Fivefold Rotation
In a quasiperiodical nuclear structure with a detectable fivefold rotational symmetry the centers of symmetry must be evenly distributed allover the structure and there must exist centers with different ranges
Optimized quasiperiodical models - like the Penrose tilings - are hierarchical systems.
In the adjacent animalistic illustrated structure 13 centers of fivefold symmetry are highlighted in turquois. The 10 centers of rotation at the border area of the image are exactly placed at the corners of a decagon. The directions of rotation alternate consequently.
Where five ochreous “turtles” put their head together there are three rotation centers with a longer range.
Girih Cartwheel
This wickerwork pattern is assembled only from two types of girih tiles, irregular hexagons and trapeziums. Their aperiodic matching rules are defined by six different colors in their corner regions. Please compare the file Girih Tiling Puzzle provided below the image.
Inside the decagon with the center point C and the top corner T the same-color corner regions are arranged to pentagons and twin pentagons with an equivalence relation to the order of a Penrose cartwheel.
The extension of this structure to the complete image area is made by four overlaps with copies of the central cartwheel. The rhombs PLVR clarify the positions of the five cartwheels.
If a red, blue or yellow colored pentagon or twin pentagon is reflected in one of the radial black lines, then the color of the mirror image is green, orange or violet.
Golden Girih Cartwheel Relievo
The opposite relievo is a digitally edited version of the predecessor image which is called «Girih Cartwheel».
The process of image editing, developed by te photographer Thomas Bischof from Nuremberg, was globally applied to the whole image, whithout any seperate change of image details.
Two png-files in high resolution of different relievo versions are provided for download. They are subject to the same open licence as other graphics of the wickerwork gallery, i. e., you have the permission to present them in non-commercial context. Attention should be paid to the best possible image quality and perpetuation of the original picture size.

Octagonal Wickerwork
The first nuclear structures with eightfold rotational symmetry were discovered in 1987. These structures are quasicrystalline because a crystalline (periodic) order may have at most a three-, four- or sixfold rotational symmetry.
A geometric description succeeds in using the Ammann-Beenker tiling. The tiles are squares and rhombs with 45°-angles. The aggregation of the smaller tiles to larger ones − visualized by the coloring − confirms the hierarchical character of the structure. The wickerwork decoration which is drawn in has a clear-cut correlation to the tiles of both scales.
The highlighted area in the image center containing two large squares and two large rhombs corresponds to one of the Gähler-octagons which cover the plane completely (with overlaps) and have a one-to-one correlation to the closed rings of the wickerwork decoration.
Color-Coded Kites and Darts
This Penrose tiling is commonly named the kite & dart tiling. Its tenfold rotational symmetry is detectable in decagonal quasicrystals.
A fourfold rotational symmetry is perfectly realized in a squared paper, i. e., the paper gives the same aspect under a 90°-rotation about a free selected point. In contrast to a squared paper the structure of a Penrose tiling isn’t based periodically. But even though the Penrose tiles are only partially assembled to symmetrical stars and decagons the aspect of the Penrose tiling doesn’t get fundamentally changed under a 36°-rotation because the kites and darts occur almost equally apportioned to the ten possible orientations.
The uniform coloring of tiles with the same orientation clarifies the quasiperiodical sequences which are characterized by a non-periodical alternation of their distances.
Please compare the image sequence directly below the graphic.
Kite Fish & Dart Rays
The figures shown in this image are composed in the manner of the artist M. C. Escher, but do not possess the periodic order characteristic of his graphic work. The arrangement of the fish and rays has been taken from the predeccessor image, a quasiperiodic and geometric Penrose tiling.
The corners of the figures correspond to the corners of the geometric tiling, whereas the edges of the tiles are deformed to the outlines of the figures.
In contrast to the geometric tiles which allow periodical arrangements too the assembling of the fish and rays force quasiperiodical order.
Two geometric tiles of the same type distinguished by a rotation of 36 degrees, correspond to mirrored figures.