The first MPE2013 exhibition featuring the winner modules of the MPE2013 competition held in collaboration with IMAGINARY takes place from March 5 – 8, 2013 at the UNESCO headquarters in Paris.
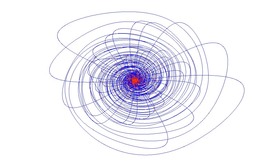
Vannerie quasi-cristalline
En 1982, le chercheur Dan Shechtman a découvert une structure d’atomes à symétrie de rotation d’ordre 5. Aujourd’hui, les structures de ce type sont appelées des quasi-cristaux.
En général, les modèles d’évolution pour les quasi-cristaux décagonaux à symétrie de rotation d’ordre 10 ou 5 sont basés sur des pavages quasipériodiques, découverts par Roger Penrose en 1973.
Pour voir de nouvelles images, cliquez sur la flèche vers la gauche!

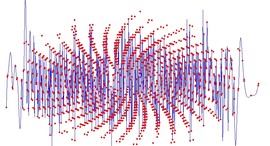
Quasicrystalline Wickerwork
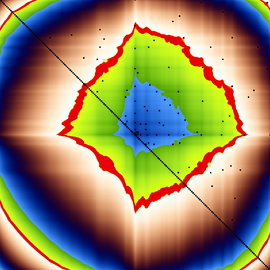
Même si le design de la vannerie à l’avant plan du graphique provient de carreaux girih de l’époque médiévale (girih en perse signifie noeud), celui-ci correspond à la structure atomique d’un quasi-cristal décagonal.
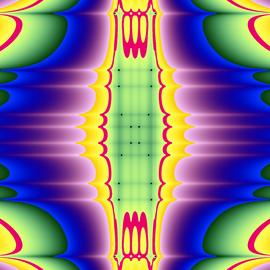
En adaptant les carreaux girih aux pavages en losanges de Penrose, ils génèrent une vannerie girih ayant en bonne approximation une symétrie rotationnelle d’ordre 10. Les nœuds fermés résultants (vert, jaune et bleu) correspondent étonnamment à la géométrie d’un modèle de couverture utilisé aujourd’hui, que l’on peut voir en arrière plan de la vannerie.
Pour une description plus détaillée de l’image, vous pouvez vous référer aux documents pdf ci-dessous (en anglais et allemand) ou sous l’image.
Cette image ainsi que d’autres de cette galerie font partie de l’exposition « IMAGINARY - Form und Formel mathematischer Fantasie » qui a été présentée pour la première fois à Nuremberg en juin 2016.
(www. imaginary.org/event/imaginary-in-nuremberg)
(www. imaginary.org/event/imaginary-at-sigena-gymnasium-in-nuremberg)
(www. imaginary.org/gallery/hand-made-hands-on)
(https://patterninislamicart.com/s/collections/main-archive/piia_image/tu…) Girih pattern in Kayseri
Woman Teaching Aperiodic Geometry
La structure sous-jacente de cette image est un pavage de Penrose quasi-périodique par des losanges, une structure géométrique utilisée pour modeler les quasi-cristaux décagonaux.
La forme de la partie en jaune présente une symétrie de rotation d’ordre 10 malgré son centre qui n’est pas de symétrie. Cette forme est communément appelé une roue.
En prenant 35 positions différentes, la jeune femme démontre ce que signifie la phrase faire la roue. Telle une allusion à l’ordre difficile d’un pavage spatial en losanges de Penrose, elle nous tourne 15 fois le dos.
Vous pouvez comparer ceci avec la chapitre III du Description Booklet dans le document pdf ci-dessous (en anglais et allemand).
Des objets pratiques illustrant un algorithme de croissance (Quasiperiodic Succession, chapitre V) avec lequel une structure de roue sans erreur peut être construite successivement peuvent être trouvés dans la seconde moitié de la galerie Hand made hands-on.
Animalistic Quasiperiodicity
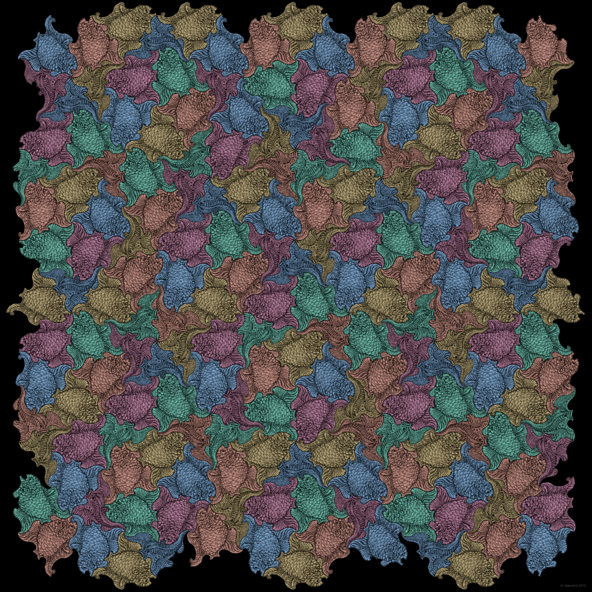
L’image ci-contre s’est inspirée de l’oeuvre renommée de l’artiste néerlandais M. C. Escher dont les figures sont jointes de manière quasi-parfaite.
Les principes d’arrangement d’Escher étaient périodiques et correspondaient à l’ordre atomique des cristaux. En revanche, l’image qui est représentée ici est basée sur un pavage de Penrose quasi-périodique. Il correspond ainsi à un ordre atomique quasi-cristallin avec une symétrie de rotation d’ordre 5, qui ne peut être cristallographique.
Les poissons en rouge nagent dans cinq orientations différentes qui diffèrent de rotations multiples de 36 degrés les unes des autres.
La couleur turquoise nous permet de deviner la forme de la roue.
Animalistic Tiling Structure
Cette image montre la correspondance entre les animaux ordonnés de manière quasi-périodique en quatre pavages différents mais dérivables ensemble.
La partie en forme d’anneau est composée de triangles jaunes et oranges, appelés les triangles de Robinson. A l’intérieur de l’anneau, les triangles sont assemblés en losanges bleus et épais, respectivements verts et étroits, d’un pavage de Penrose, tandis que l’extérieur est formé de cerfs-volants bleus et de fléchettes vertes.
Chaque cerf-volant est en correspondance avec un pentagone bleu, vert ou jaune du pavage de Penrose pentagonal de l’arrière-plan. Le coin concave d’une fléchette se trouve toujours au centre d’un pentagone noir, la tête de la flèche au centre d’un violet. Les points blancs et noirs représentent les points de rencontre des cerfs-volants & fléchettes.
Animalistic Fivefold Rotation
Dans une structure atomique avec une symétrie d’ordre 5, les centres de symétrie doivent être distribués sur toute la structure et il doit y avoir des centres avec des portées différentes.
Les modèles quasi-périodiques optimisés, tels les pavages de Penrose, sont des systèmes hiérarchisés.
Dans la structure ci-contre illustrée d’animaux, 13 centres de symétrie d’ordre 5 sont mis en valeur en turquoise. Les dix centres de rotation vers la frontière de l’image sont placés exactement sur les côtés d’un décagone, avec une alternance des directions de rotation.
Trois centres de symétrie avec des portées plus longues se trouvent là où cinq «tortues» de couleur ocre joignent leurs têtes.
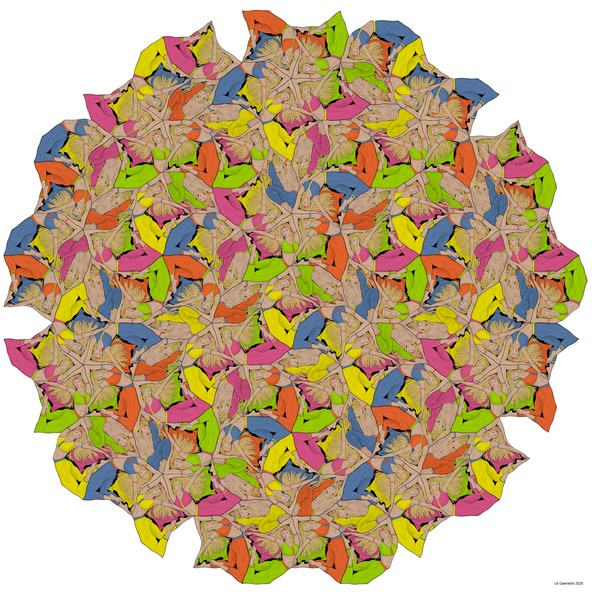
Girih Cartwheel
Ce motif de vannerie est assemblé seulement à partir de deux types de pavages girih, des héxagones irréguliers et des trapèzes. Leur disposition apériodique est définie par six couleurs différentes pour leurs coins. Vous pouvez comparer ceci avec le fichier Girih Tiling Puzzle au-dessous de l’image.
A l’intérieur du décagone composé du point central C et du coin supérieur T, les coins de couleur identique sont disposés en pentagones simples et doubles avec une relation d’équivalence de l’ordre d’une roue de Penrose.
L’extension de cette structure à toute la surface de l’image est composée de quatre chevauchements avec des copies de la roue centrale. Les losanges de sommets PLVR indiquent les positions de celles-ci.
Si un pentagone simple ou double de couleur rouge, bleu ou jaune est réfléchi par l’une des lignes noires radiales, la couleur de l’image sera verte, orange ou violette respectivement.
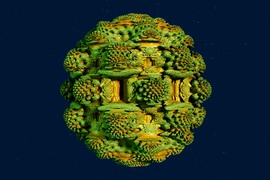
Golden Girih Cartwheel Relievo
L’enlevure ci-contre est une version façonnée digitalement de l’image précédente, entitulée «Girih Cartwheel».
Le procédé du façonnage, développé par le photographe Thomas Bischof de Nuremberg, était appliqué globalement à l’image entière, sans quelques changements particuliers sur détails d’image.
Deux fichiers (png) en haute résolution de differentes versions d’enlevure sont préparés pour téléchargement. Ils sont soumis à la même licence ouverte comme les autres graphiques du galerie de vannerie, c’est-à-dire vous êtes autorisés de présenter les images sous tous rapports non-commerciaux, en respectant le meilleure qualité d’image et le maintien du format original.

Octagonal Wickerwork
Les premières structures atomiques composées de symétrie de rotation d’ordre 8 ont été découvertes en 1987. Ces structures sont quasi-cristallines parce qu’un ordre cristallin (périodique) ne peut avoir qu’une symétrie rotationnelle d’ordre 3, 4 ou 6.
Une description géométrique a été rendue possible grâce au pavage d’Ammann-Beenker. Les motifs sont des carrés et losanges avec des angles de 45 degrés. La réunion des petites figures en les grandes (visibles par leurs couleurs) confirme le caractère hiérarchisé de la structure. La vannerie dessinée en décoration admet une corrélation précise avec les motifs des différentes tailles .
La région mise en valeur dans l’image du centre contenant deux grands carrés et quatre grands losanges correspond à l’un des octogones de Gähler qui recouvrent complètement la surface (avec des chevauchements) et sont en correspondance avec les anneaux fermés de la vannerie décorative.
Color-Coded Kites and Darts
Le pavage de Penrose montré ici est bien connu sous le nom de kite & dart (cerf-volant & fléchette). Sa symétrie de rotation d’ordre 10 est décelable pour les quasi-cristaux décagonaux.
Dans un papier à carreaux, une symétrie de rotation d’ordre quatre est parfaitement réalisée, c’est-à-dire que le papier offre à nouveaux la même vue après une rotation de 90° autour d’un point au choix. Contrairement au papier à carreaux, le pavage de Penrose n’a pas de structure périodique. Mais bien que ses éléments s’assemblent seulement en partie en des étoiles symétriques et des décagones, l’apperance du pavage ne se change pas fondamentalement sous une rotation de 36°, puisque les cerfs-volants et fléchettes sont presque aussi communs dans les dix orientations possibles.
La coloration uniforme des éléments de même orientation fait ressortir les arrangements quasi-périodique, qui sont caractérisés par la suite non-périodique de leurs distances.
Veuillez comparer la séquence d’images directement sous le graphique.
Kite Fish & Dart Rays
Les figures de cette image sont disposées à la manière de l’artiste M. C. Escher, mais n’ont pas l’ordre périodique qui caractérise son œuvre graphique. La disposition des poissons et des raies est dérivé de l’image précédente, un pavage de Penrose quasi-périodique et géométrique.
Les coins des figures correspondent aux coins du pavage géométrique, tandis que les bords des tuiles sont déformés aux contours des figures.
Contrairement aux tuiles géométriques, qui permettent également des pavages périodiques, le placement parfait des poissons et les raies impose un ordre quasi-périodique.
Deux tuiles géométriques du même type, distinguées par une rotation de 36 degrés, ont un équivalent en deux figures qui sont des images miroir l’une de l’autre.