The National Institute for Mathematical Sciences (NIMS) presents a very special NIMS-IMAGINARY exhibition in collaboration with the ICM committee and the Mathematisches Forschungsinstitut Oberwolfach (MFO). It will feature the best of all IMAGINARY modules of the last years and a lot of new software, images, films and sculptures. It will be the biggest IMAGINARY exhibition shown so far.
Kuazi Kristal Hasır İşi
1982›de Dan Shechtman, beş kat rotasyonel simetriye sahip nükleer bir yapı keşfetti. Bu tür yapılara kuazikristaller denir.
Genel olarak, on kat (veya beş kat) dönme simetrisine sahip dekagonal kuazikristaller için büyüme modelleri, 1973 yılında Roger Penrose tarafından icat edilen geometrik, kuaziperiyodik parkelere dayanmaktadır.

Kuazi kristal bir Hasır İşi
Hasır işi, ortaçağ girih şablonları (Topkapı Sarayı’nda görülenler gibi) kullanılarak büyük grafiğin ön planında yaratılmış olsa da, desenin dekagonal bir kuazikristalin atomik yapısıyla bir ilişkisi vardır.
Girih şablonlarını modern bir elmas-Penrose parke üzerine yerleştirerek, on kat dönme simetrisine iyi karşılık gelen bir Girih ağı oluşturuldu. Şaşırtıcı bir şekilde, üç kapalı düğüm vardır (yeşil, sarı ve mavi). Ağın arka planında görülebilen şu anda kullanılan bir kapsama modelinin geometrik yapısına tam olarak karşılık gelirler.
Ayrıntılı bir açıklama için lütfen aşağıda verilen PDF belgelerine (Almanca İngilizce) veya resmin altındaki dosyalara bakın.
Bu grafik ve bu galerinin diğer bazı resimleri «IMAGINARY - Form und Formel mathematischer Fantasie» sergisinin bir parçasıdır. Bu sergi ilk kez Haziran 2016›da Nürnberg’de gösterildi.
(www. imaginary.org/event/imaginary-in-nuremberg)
(www. imaginary.org/event/imaginary-at-sigena-gymnasium-in-nuremberg)
(www. imaginary.org/gallery/hand-made-hands-on)
(https://patterninislamicart.com/s/collections/main-archive/piia_image/tu…) Girih pattern in Kayseri
Periyodik Olmayan Geometri Öğreten Kadın
Bu görüntünün temelini oluşturan yapı, dekagonal kuazikristallerin modellenmesinde kullanılan geometrik bir yapı olan kuaziperiyodik (aperiyodik) eşkenar dörtgen-penroz parkesidir.
Sarı renkli alanın ana hatları, iç kısmı asimetrik olmasına rağmen, on kat dönme simetrisine sahiptir. Bu düzenlemeye cartwheel (Türkçe tekerleği) denir.
35 farklı pozisyonla genç kadın bize bir tekerleğe nasıl çarpacağımızı gösteriyor. Pastillerin mekansal bir Penrose parkesindeki düzenlemesine bir ima olarak, kadın bize 15 kez sırtını dönüyor.
Lütfen aşağıda pdf belge olarak bulunan açıklayıcı broşürün III. Bölümüne de bakınız (ALMANCA/İNGİLİZCE).
Hatasız bir yapının birbiri ardına inşa edilebildiği bir büyüme algoritması (Kuaziperiyodik Ardıllık, Bölüm V) gösteren uygulamalı nesneler, aşağıdaki galerinin ikinci yarısında bulunabilir.
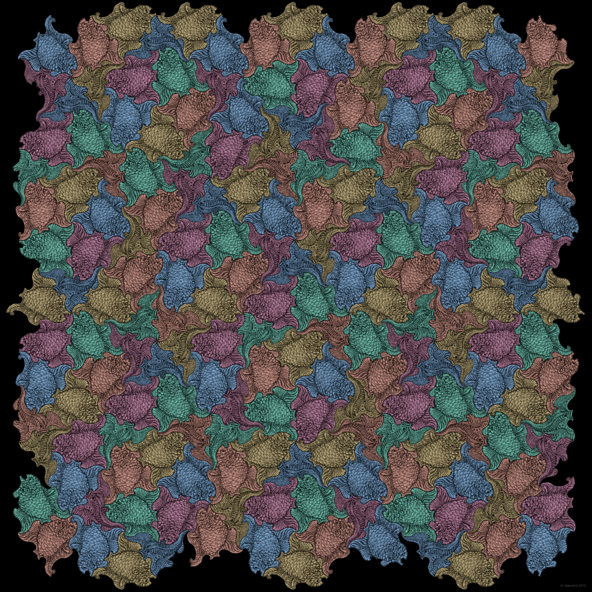
Kuaziperiyodik Hayvan Desenleri
Bu resim, kendi figürlerini buna benzer hatasız bir biçimde birleştiren Hollandalı ünlü ressam M. C. Escher’in çok bilinen eserinden ilhamını almıştır.
Bununla birlikte, Escher’in şekil düzenlemeleri dönemseldir ve kristallerin atomik düzenlemelerine karşılık gelir. Ancak gördüğümüz bu resim kuaziperiyodik bir Penrose parkesine dayanıyor. Yani, beş katlı dönme simetrisine sahip kuazikristalin bir atomik kafese karşılık gelir ve bu düzenleme kristalografik olamaz.
Kırmızı renkli balıklar, birbirine 36 derecelik açılarla döndürülmüş 5 farklı doğrultuda yüzüyor.
Hayvanların turkuaz rengi, bir vagon tekerleğinin tekerlek göbeğinin şeklini tanımamızı sağlar.
Hayvan Desenli Döşeme
Bu resim, kuazi periyodik olarak düzenlenmiş hayvanların birbirinden türetilebilen dört farklı parkeye oranını göstermektedir.
Halka şeklindeki alan, hayvan desenleriyle dolu Robinson üçgenleri adı verilen sarı ve turuncu üçgenlerden oluşur. Halka içinde, üçgenler mavi kalın ve yeşil dar Penrose eşkenar dörtgenleri olarak gruplandırılmıştır. Halkanın dışında, mavi uçurtmalar ve yeşil ok uçları halinde gruplandırılırlar.
Tüm ejderhaların arka planda Penrose Pentagon paketinin mavi, yeşil veya sarı beşgeni ile bire bir ilişkisi vardır. Bir okun içbükey köşesi her zaman siyah bir beşgenin ortasında, ok ucu mor olanın ortasındadır. Beyaz ve siyah noktalar, ejderhaların ve okların bileşimi için kuralları temsil eder.
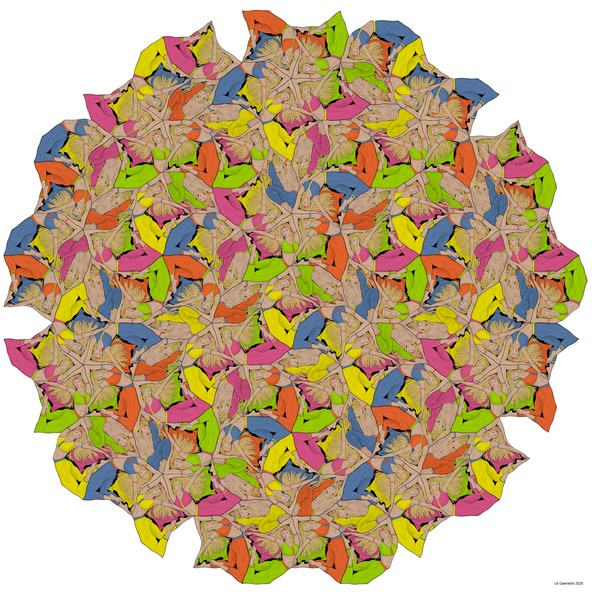
Hayvan Desenli Beşli Döndürme
Beş katlı bir simetrinin tespit edilebildiği kuazi kristalin bir atomik yapıda, simetri merkezleri tüm yapıya eşit olarak dağıtılmalı ve farklı boyutlarda merkezler bulunmalıdır.
Penrose parkeleri optimize edilmiş kuaziperiyodik modeller olduğundan, hiyerarşik bir yapıya sahip olmaları gerekir!
Hayvan desenleri ile yapılan bu çizimde, turkuaz renkte beş kat dönme simetrisine sahip 13 merkez vurgulanmıştır. Bunlardan 10 tanesi tam olarak resmin kenarındaki normal bir dekagon’un köşelerinde bulunur. Bu merkezlerde dönme yönü düzenli olarak değişir.
Aşı boyası renkli «kaplumbağaların» beşinin kafalarını topladığı yerde, daha geniş menzile sahip üç dönme merkezi vardır.
Girih Cartwheel
Bu hasır işi süsleme sadece iki girih tuğla çeşidinden, düzensiz altıgenlerden ve yamuklardan oluşuyordu. Yapı taşlarının periyodik olmayan uygulama kuralları köşe alanlarında altı farklı renkle tanımlanmaktadır. Lütfen resmin altındaki Girih Tiling Puzzle dosyasını karşılaştırın.
Merkez C ve üst köşe T ile karakterize edilen dekagonal şekilde, Girih taşları aynı renkteki köşe alanlarında beşgenlere ve ikizlere birleştirildi, böylece sonuç bir Penrose-cartwheel oldu.
Bu yapının tüm görüntü alanı boyunca genişletilmesi, orta Penrose cartwheel dört kopya ile kaplanmasıyla gerçekleştirildi. PLVR elmasları beş Penrose cartwheels konumunu gösterir.
Radyal siyah çizgilerden birine kırmızı, mavi veya sarı beşgen bir şekil yansıtıldığında, yansıması yeşil, turuncu veya mordur.
Golden Girih Cartwheel Relievo
Burada gösterilen rölyef çalışması, «Girih Cartwheel» başlıklı önceki grafiğin dijital olarak düzenlenmiş bir versiyonudur.
Nürnbergli fotoğrafçı Thomas Bischof tarafından geliştirilen işleme yöntemi, görüntü ayrıntılarına ayrı bir müdahale yapılmaksızın tüm görüntüye küresel olarak uygulandı.
İki farklı kabartma sürümünden iki yüksek çözünürlüklü png dosyası indirilebilir. Wickerwork Gallery’deki diğer grafiklerle aynı açık lisansa tabidirler, yani mümkün olan en iyi görüntü kalitesine ve orijinal formatın korunmasına özen göstererek ticari olmayan tüm bağlamlarda gösterilebilirler.

Octagonal Wickerwork
Sekiz kat rotasyonel simetriye sahip ilk atomik yapılar 1987›de keşfedildi. Bu yapılar kuazikristalindir, çünkü kristalin (periyodik) bir düzen maksimum üç, dört veya altı kat dönme simetrisine sahip olabilir.
Ammann-Beenker parke ile geometrik bir açıklama başarılı olur. Yapı taşları 45°›lik bir açıyla kare veya eşkenar dörtgendir. Daha küçük yapı taşlarının daha büyük yapı taşlarına renk görünür kombinasyonu, yapının hiyerarşik karakterini gösterir. Ön plandaki örgü deseni, her iki boyuttaki yapı taşlarıyla doğrudan ilgilidir.
İki büyük kare ve dört büyük eşkenar dörtgen içeren görüntünün ortasındaki aydınlatılmış alan, yüzeyi tamamen kaplayan (üst üste binen) ve hasır işçiliğinin kapalı halkalarıyla bire bir ilişkisi olan Gähler sekizgenlerinden birine karşılık gelir.
Color-Coded Kites and Darts
Burada gösterilen Penrose parkesi Kites and Dart olarak bilinir. Parkenin on kat dönme simetrisi dekagonal kuazi kristallerde tespit edilebilir.
Damalı bir kağıt üzerinde, dörtlü bir dönme simetrisi mükemmel bir şekilde gerçekleştirilir, böylece kağıt serbestçe seçilebilir bir nokta etrafında 90 ° dönüldükten sonra tekrar aynı görünüme sahip olur. Damalı kağıdın aksine, Penrose parke periyodik bir yapıya sahip değildir. Ancak, yapı taşları rotasyonel olarak simetrik yıldızlar veya dekagonlar oluşturmak için sadece kısmen bir araya gelse de, ejderhalar ve oklar on olası yönelimin hepsinde neredeyse eşit sıklıkta temsil edildiğinden, görünümü 36 ° ‹lik bir dönüşten sonra temelde değişmez.
Yapı taşlarının belirli bir yönelime sahip düzgün bir şekilde renklendirilmesi yoluyla, mesafelerin karakteristik, periyodik olmayan varyasyonlarına sahip kuazi periyodik diziler açıkça görülebilir hale gelir.
Lütfen dosyayı tablonun hemen altındaki resim serisiyle karşılaştırın.
Kite Fish & Dart Rays
Bu resimdeki figürler, sanatçı M. C. Escher’in tarzında bestelenmiştir, ancak grafik çalışmasının periyodik düzen özelliğine sahip değildir. Balıkların ve ışınların düzenlenmesi, kuazi-periyodik ve geometrik bir Penrose parke olan önceki resimden alınmıştır.
Figüratif yapı taşlarının köşeleri geometrik parkenin köşelerine karşılık gelir, ancak geometrik yapı taşlarının düz kenarları figüratif tuğlalarda deforme olur.
Geometrik yapı taşları ayrıca periyodik bileşimlere izin verirken, balık ve ışınların konturları kuazi periyodik bir diziyi zorlar.
Birlikte 36 ° daha fazla döndürülen aynı tipteki iki geometrik yapı taşı, ayna ters çevrilmiş şekillerdeki karşılıklarına sahiptir.