Das National Institute of Mathematical Sciences (NIMS) stellt in Zusammenarbeit mit dem ICM-Komitee und dem Mathematischen Forschungsinstitut Oberwolfach (MFO) eine besondere IMAGINARY-Ausstellung vor. Gezeigt werden die besten IMAGINARY-Module der letzten Jahre und eine Vielzahl neuer Softwareprogramme, Bilder, Filme und Skulpturen. Es handelt sich um die bislang größte IMAGINARY-Ausstellung.
Quasicrystalline Wickerwork
Im Jahr 1982 entdeckte Dan Shechtman eine Kernstruktur mit einer fünffachen Rotationssymmetrie. Heutzutage werden Kernstrukturen dieser Art Quasikristalle genannt.
Zumeist beruhen Wachstumsmodelle für dekagonale Quasikristalle mit zehn- oder fünffacher Rotationssymmetrie auf geometrischen, quasiperiodischen Parketten, die ab 1973 von Roger Penrose entwickelt wurden.
Für neue Bilder drücke den linken Pfeil!

Quasicrystalline Wickerwork
Obwohl das Flechtwerk im Vordergrund der großen Grafik aus mittelalterlichen Girih-Schablonen zusammengesetzt worden ist (persich Girih, dt. Knoten), besitzt es eine Beziehung zu der Atomstruktur eines dekagonalen Quasikristalls.
Durch die Einpassung der Girih-Schablonen in ein modernes Rhomben-Penrose-Parkett wurde ein Girih-Flechtwerk mit einer gut angenäherten zehnzähligen Drehsymmetrie erzeugt. Die dabei entstehenden geschlossenen Knoten (grün, gelb und blau) korrespondieren überraschenderweise mit der Geometrie eines Überdeckungsmodells, das im Hintergrund des Flechtwerks zu sehen ist.
Ausführliche Beschreibungen zu diesem Bild finden Sie weiter unten bei den pdf-Dokumenten (DEUTSCH/ENGLISCH) und direkt unter dem Bild.
Diese Grafik und einige andere Bilder dieser Galerie sind Teil der Ausstellung „IMAGINARY - Form und Formel mathematischer Fantasie“, die erstmals im Juni 2016 in Nürnberg gezeigt wurde.
(www. imaginary.org/event/imaginary-in-nuremberg)
(www. imaginary.org/event/imaginary-at-sigena-gymnasium-in-nuremberg)
(www. imaginary.org/gallery/hand-made-hands-on)
(https://patterninislamicart.com/s/collections/main-archive/piia_image/tu…) Girih pattern in Kayseri
Woman Teaching Aperiodic Geometry
Die diesem Bild unterlegte Struktur ist ein quasiperiodisches (aperiodisches) Rhomben-Penrose-Parkett, eine geometrische Struktur, die bei der Modellierung dekagonaler Quasikristalle zur Anwendung kommt.
Der Umriss des gelb eingefärbten Bereichs besitzt eine zehnzählige Drehsymmetrie, obwohl sein Inneres asymmetrisch ist. Diese Anordnung wird cartwheel (dt. Wagenrad) genannt.
Mit ihren 35 unterschiedlichen Positionen demonstriert uns die junge Frau, wie man ein Rad schlägt (engl. doing a cartwheel). Als eine Anspielung auf die komplizierte Ordnung eines räumlichen, rhomboedrischen Penrose-Parketts kehrt sie uns dabei 15 mal den Rücken zu.
Bitte vergleichen Sie auch Kapitel III des description booklet (DEUTSCH/ENGLISCH), das Sie weiter unten als pdf-Dokument finden.
Hands-on-Objekte, die einen Wachstums-Algorithmus (Quasiperiodic Succession, Kapitel V) veranschaulichen, mit dem sukzessiv eine fehlerfreie Cartwheel-Struktur aufgebaut werden kann, finden Sie in der zweiten Hälfte der Galerie Hand made hands-on.
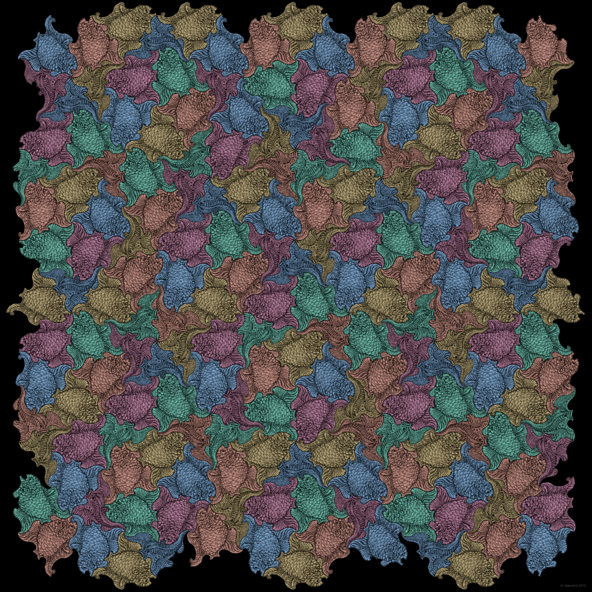
Animalistic Quasiperiodicity
Als Vorbild für das nebenstehende Bild dienten die hervorragenden Arbeiten des bekannten niederländischen Künstlers M. C. Escher, der seine Figuren in entsprechender lückenloser Weise aneinanderfügte.
Während Eschers Ordnungsprinzipien jedoch periodisch sind und somit eine Entsprechung zu kristallinen Atomgittern besitzen, ist das hier gezeigte Bild auf einem quasiperiodischen Penrose-Parkett aufgebaut, das einem quasikristallinen Atomgitter mit fünffacher Drehsymmetrie entspricht, das deshalb nicht kristallographisch sein kann.
Die rot eingefärbten Fische schwimmen in fünf unterschiedlichen Orientierungen, die jeweils um 36 Grad zueinander gedreht sind.
Die türkise Einfärbung lässt uns die Form der Nabe eines Wagenrades erkennen.
Animalistic Tiling Structure
Dieses Bild zeigt die Beziehung der quasiperiodisch angeordneten Tiere zu vier unterschiedlichen, aber wechselseitig voneinander ableitbaren Parketten.
Die gelben und orangen Dreiecke, aus denen der ringförmige Bereich besteht, nennt man Robinson-Dreiecke. Innerhalb des Ringes sind die Dreiecke zu dicken blauen und dünnen grünen Penrose-Rhomben zusammengefasst worden, außerhalb zu blauen Drachen und grünen Pfeilen (kite & dart).
Alle Drachen haben eine Eins-zu-eins-Beziehung zu einem blauen, grünen oder gelben Fünfeck des Penrose-Pentagon-Parketts im Hintergrund. Die konkave Ecke eines Pfeils liegt immer im Zentrum eines schwarzen Fünfecks, die Pfeilspitze im Zentrum eines violetten. Die weißen und schwarzen Punkte repräsentieren die Anlegeregeln der Drachen und Pfeile.
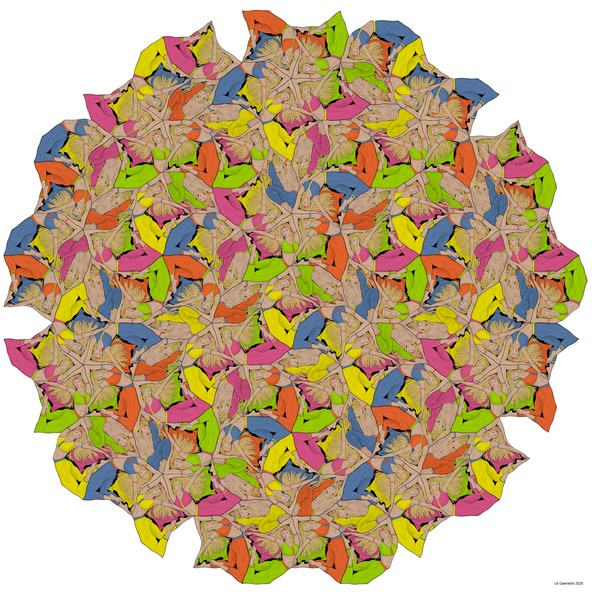
Animalistic Fivefold Rotation
In einer quasikristallinen atomaren Struktur, für die eine fünffache Symmetrie nachwiesen werden kann, müssen die Symmetriezentren über die gesamte Struktur hinweg gleichmäßig verteilt sein und es müssen Zentren mit unterschiedlichen Reichweiten existieren.
Optimierte quasiperiodische Modelle, wie die Penrose-Parkette, sind hierarchische Systeme!
In dem nebenstehenden animalistisch illustrierten Strukturbeispiel sind 13 Zentren fünffacher Symmetrie türkis hervorgehoben. Die 10 Zentren am Bildrand befinden sich exakt auf den Ecken eines Zehnecks. Die Drehrichtungen der Symmetriezentren wechseln sich konsequent ab.
Dort, wo jeweils fünf der ockerfarbenen „Schildkröten“ ihre Köpfe zusammenstecken, befinden sich drei Drehzentren mit größerer Reichweite.
Girih Cartwheel
Dieses Flechtwerksornament wurde aus nur zwei Girih-Bausteinsorten zusammengesetzt, unregelmäßigen Sechsecken und Trapezen. Die aperiodischen Anlegeregeln der Bausteine werden durch sechs verschiedene Farben in ihren Eckbereichen definiert. Bitte vergleichen Sie die Datei Girih Tiling Puzzle unterhalb des Bildes.
Innerhalb des Zehnecks mit dem Mittelpunkt C und dem oberen Eckpunkt T wurden jeweils gleichfarbige Eckbereiche so zu Fünfecken und Fünfeckzwillingen zusammengefügt, dass sie einem Penrose-Cartwheel entsprechen.
Die Erweiterung dieser Struktur auf den gesamten Bildbereich entstand durch vier Überdeckungen mit Kopien des zentralen Cartwheels. Die Rhomben PLVR zeigen die Lage der fünf Cartwheels.
Wenn eine rote, blaue oder gelbe Fünfeckform an einer der radialen schwarzen Linien gespiegelt ist, dann ist ihr Spiegelbild grün, orange oder violett.
Golden Girih Cartwheel Relievo
Die nebenstehende Reliefarbeit ist eine digital bearbeitete Version der vorhergehenden Grafik mit dem Titel «Girih Cartwheel».
Das von dem Nürnberger Fotografen Thomas Bischof entwickelte Bearbeitungsverfahren wurde global auf das gesamte Bild angewandt, ohne irgendwelche separaten Eingriffe in die Bilddetails.
Zwei hochauflösende png-Dateien von zwei unterschiedlichen Relief-Versionen können heruntergeladen werden. Sie unterliegen der gleichen, offenen Lizenz wie die anderen Grafiken der Wickerwork-Galerie, d. h., sie dürfen in allen nicht-kommerziellen Zusammenhängen gezeigt werden, wobei auf bestmögliche Bildqualität und die Beibehaltung des Originalformats zu achten ist.

Octagonal Wickerwork
Die ersten atomaren Strukturen mit achtzähliger Drehsymmetrie wurden 1987 entdeckt. Diese Strukturen sind quasikristallin, da eine kristalline (periodische) Ordnung höchstens eine drei-, vier- oder sechszählige Drehsymmetrie besitzen kann.
Eine geometrische Beschreibung gelingt über das Ammann-Beenker-Parkett. Dessen Bausteine sind Quadrate und Rhomben mit 45°-Winkeln. Die farblich sichtbar gemachte Zusammenfassung der kleineren Bausteine zu größeren untermauert den hierarchischen Charakter der Struktur. Das eingezeichnete Flechtwerksmuster hat einen direkten Bezug zu den Bausteinen beider Größen.
Der aufgehellte Bereich in der Bildmitte, der zwei große Quadrate und vier große Rhomben beinhaltet, entspricht einem der Gähler-Oktogone, die die Fläche vollständig überdecken (mit Überlappungen) und eine Eins-zu-eins-Beziehung zu den geschlossenen Ringen des Flechtwerks besitzen.
Color-Coded Kites and Darts
Das hier gezeigte Penrose-Parkett ist unter dem Namen kite & dart (Drachen & Pfeil) bekannt. Seine zehnzählige Drehsymmetrie ist in dekagonalen Quasikristallen nachweisbar.
In einem karierten Papier ist eine vierzählige Drehsymmetrie perfekt realisiert, d. h., das Papier bietet nach einer 90°-Drehung um einen frei wählbaren Punkt wieder denselben Anblick. Das Penrose-Parkett besitzt, im Gegensatz zum karierten Papier, keinen periodischen Aufbau. Aber obwohl sich seine Bausteine nur teilweise zu drehsymmetrischen Sternen bzw. Zehnecken zusammenfinden, verändert sich sein Anblick nach einer 36°-Drehung dennoch nicht grundsätzlich, da die Drachen und Pfeile in allen zehn möglichen Orientierungen annähernd gleich häufig vertreten sind.
Die einheitliche Einfärbung von Bausteinen mit einer bestimmten Orientiertierung macht die quasiperiodischen Reihungen mit dem charakteristischen, nicht periodischen Wechsel der Abstände deutlich sichtbar.
Bitte vergleichen Sie dazu die Datei mit der Bildsequenz direkt unter der Grafik.
Kite Fish & Dart Rays
Die Figuren auf diesem Bild sind in der Manier des Künstlers M. C. Escher zusammengesetzt, besitzen aber nicht die periodische Ordnung, die charakteristisch für sein grafisches Werk ist. Die Anordnung der Fische und Rochen ist vom vorhergehenden Bild übernommen worden, einem quasiperiodischen und geometrischen Penrose-Parkett.
Die Ecken der Figuren entsprechen den Ecken des geometrischen Parketts, jedoch sind die geraden Kanten der geometrischen Bausteine bei den figürlichen Bausteinen verformt.
Während die geometrischen Bausteine auch periodische Zusammenstellungen zulassen, erzwingt das Aneinanderlegen der Fische und Rochen eine quasiperiodische Ordnung.
Zwei geometrische Bausteine desselben Typs, die um 36° zueinender gedreht sind, haben ihre Entsprechung in spiegelverkehrten Figuren.