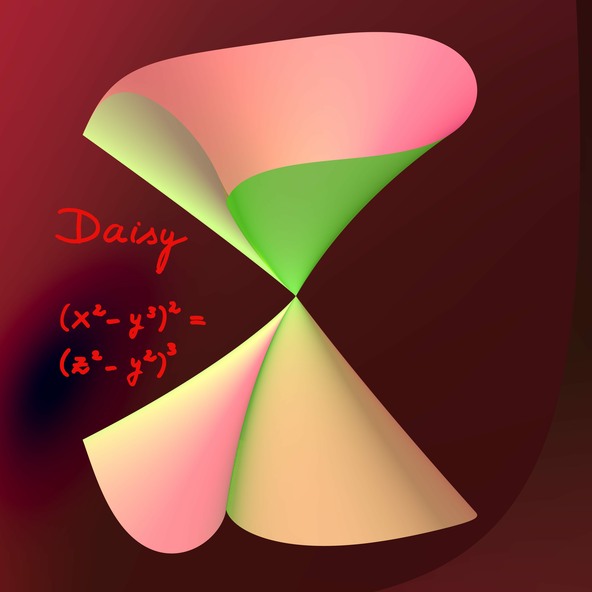Mathe kann schön sein! Am 6. Juli werden um 11:00 Uhr zwei neue interaktive Stationen im EXPERIMINTA ScienceCenter in Frankfurt a. M. vorgestellt. An der Eröffnung werden Prof. Oldenburg von der Goethe-Universität Frankfurt und Dr. Matt vom Mathematischen Forschungsinstitut Oberwolfach teilnehmen. Die beiden Stationen werden von einer Galerie schöner Visualisierungen ergänzt und sind im ScienceCenter dauerhaft zu sehen.
Herwig Hausers klassische algebraische Flächen
Herwig Hausers klassische algebraische Flächen wurden für die original IMAGINARY Ausstellung entwickelt. Seine Formeln und Formen zeichnen sich durch einfache Gleichungen und schöne natürliche Flächen aus, an denen viele interessante geometrische Phänomene zu sehen sind.
Herwig Hauser ist Mathematik-Professor an der Universität Wien und forscht auf den Gebieten Algebraische Geometrie und Singularitätentheorie.
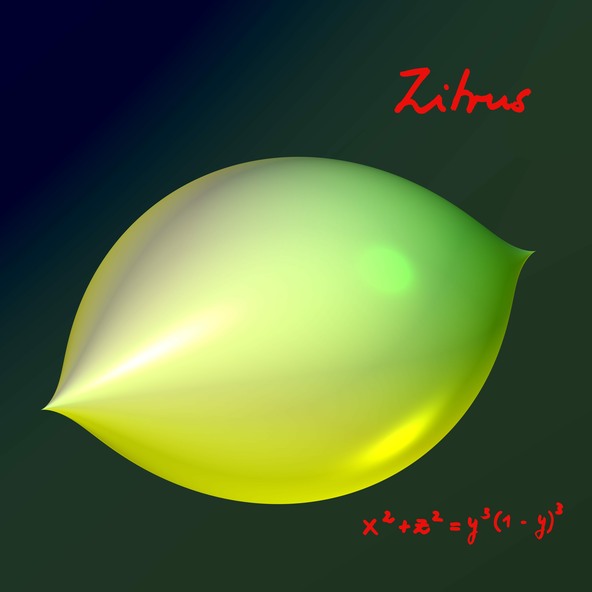
Zitrus (citric)
Die Gleichung x2+z2 = y3(1−y)3 von Zitrus erscheint ebenso einfach, wie die Figur selbst. Zwei spiegelsymmetrisch angeordnete Spitzen rotieren um die durch sie gehende Achse. Die durch Weglassen von (1−y)3 vereinfachte Gleichung x2+z2 = y3 sorgt für genau eine Spitze und x2+z2 = (1−y)3 liefert das Spiegelbild. Beide sind unendlich ausgedehnte Flächen. Das Produkt auf der rechten Seite der ursprünglichen Gleichung bewirkt, dass Zitrus beschränkt bleibt. Man kann sich überlegen: Wird y dem Betrag nach größer als 1 und damit die rechte Seite negativ, so erlaubt die Gleichung keine reellen Lösungen für x und z.
Limão
Diese Fläche mit der Gleichung x2=y3z3 ist nur schwer in ansprechender Weise zu visualisieren. Sowohl die Beleuchtung als auch die Ausformung in der Nähe des Ursprungs machen Probleme. Die Abbildung soll ja möglichst authentisch die Figur wiedergeben. Dies hängt von der Geometrie und vor allem vom Blickwinkel der kamera ab. Hin und wieder entstehen Artefakte, wie Ausfransungen oder melierte Färbungen, die nicht der mathematischen Realität entsprechen. Auch Reflexionen können störend wirken. Längs der Kanten bilden sich in der Nähe des Schnitt-punktes Nebel, trotz der Qualität des programms POVRay. Das Problem liegt vielmehr in der Komplexität, Gleichungen in der Nähe von singulären Punkten zu lösen. Die sogenannte Auflösung der Singularitäten, die eine Parametrisierung der Flache liefert, kann hier in vielen Fällen weiterhelfen.
Vis à Vis
Vis à Vis heißt Gegenüber - und hier stehen sich zwei wesentliche Phänomene der algebraischen Geometrie gegenüber. Die singuläre Spitze links schaut auf einen gewölbten, aber glatten Hügel rechts. Die Singularität ist spannender, da etliche Änderungen der Gleichung unvorhersehbare Änderungen der Form bewirken können, was bei glatten Stellen nicht passiert. Mit dem Programm SURFER, das unter http://imaginary.org/program/surfer frei erhältlich ist, kann man solche Flächen ganz einfach und intuitiv selbst herstellen und verändern. Die Gegenüberstellung von Form und Formel, also der Gleichung und der dazugehörigen Fläche, wird so zum interaktiven Erlebnis und dadurch noch anschaulicher.
Calypso
Die Fläche Calypso mit Gleichung x2+y2z = z2 enthält drei Geraden. Die horizontale Gerade ist klar ersichtlich, sie geht durch den Ursprung 0, in dem sich der obere und der untere Teil berühren. Die zwei anderen Geraden liegen in einer vertikalen Ebene, sie gehen ebenfalls durch 0 und schneiden sich dort. Der Schnitt der Fläche mit dieser Ebene zeigt die beiden Geraden. Verschiebt man diese Ebene etwas nach vorne, so wird die Schnittkurve zu einer Hyperbel. Dies lässt sich leicht durch Rechnung nachprüfen, indem man in der Gleichung entweder y = 0 oder y = 1 setzt. Im ersten Fall ergibt sich x2 = z2 oder (x−z)(x + z) = 0, die Gleichung von zwei Geraden in der Ebene. Im zweiten Fall erhält man x2+z = z2. Dies lässt sich in −x2+(z−1/2)2 = 1/4 umschreiben, die Gleichung einer Hyperbel mit Zentrum in (0, 1/2).
Calyx
Die Fläche Calyx mit Gleichung x2+y2z3 = z4 hat eine Gerade als singulären Ort. Der untere Teil der Fläche hat spitzenartige Singularitäten entlang dieser Geraden, wohingegen der obere Teil die Gerade in einem Punkt, dem Ursprung, tangential berührt. Das reelle Bild ist insoweit irreführend, als dass das definierende Polynom irreduzibel ist und die Fläche daher aus nur einer algebraischen Komponente besteht (und nicht aus zwei Komponenten, wie die Abbildung suggeriert). Man kann zeigen, dass Calyx eine geeignete Projektion von Calypso ist. Hierbei wird eine Zylinderfläche im dreidimensionalen Raum auf die singuläre Gerade von Calyx kontrahiert. Algebraisch ist die Abbildung durch die Vorschrift (x, y, z) → (xz, y, z) gegeben. Sie ist sehr einfach. Die entsprechende Substitution in x2+y2z3 = z4 und anschließendes Kürzen von z2 liefert die Gleichung x2+y2z = z2 von Calypso.
Daisy
Aus der Gleichung (x2−y3)2 = (z2−y2)3 von Daisy schließt man durch Differentiation, dass der singuläre Ort aus zwei (ebenen) Spitzkurven besteht, die sich in ihrem gemeinsamen singulären Punkt transversal treffen. Um die Singularitäten besser zu verstehen, konstruiert der Geometer ihre Auflösung mittels Explosionen. Sie liefern in endlich vielen Schritten eine Fläche ohne Singularitäten (eine Mannigfaltigkeit), zusammen mit einer Abbildung auf die ursprüngliche Fläche, die diese als Schatten der Mannigfaltigkeit unter einer Projektion interpretiert.
Diabolo
Die Gleichung x2 = (y2+z2)2 von Diabolo zerfällt in das Produkt ( −y2−z2)(x+y2+z2) = 0. Folglich ist die zugehörige Fläche die Vereinigung der beiden einschaligen Drehhyperboloide x = ±(y2+z2). Sie berühren sich im Nullpunkt tangential. Die Berührung erkennt man algebraisch am übereinstimmenden linearen Term x in den beiden Faktoren. Die Tangentialebene ist die vertikale Ebene x = 0. Die Streifen in den Abbildungen sind Schatten, die von der Beleuchtung herrühren. Stört man die Gleichung von Diabolo durch Addition eines konstanten Terms wie in x2 = (y2+z2)2+1/1000, so werden die beiden Hälften getrennt. Die Substitution von x durch x+y liefert hingegen die Variation (x+y)2 = (y2+z2)2 der Gleichung. Sie verschiebt die beiden Schalen schräg zueinander.
Ding Dong
Diese Fläche mit der Gleichung x2+y2+z3=z2 war eine der allerersten Visualisierungen, die wir versuchten. Gleichung und Form sind einfach: eine vertikal gestellte Alpha-Schleife rotiert um die z-Achse. Das Problem bestand in der Färbung. Grün ist prinzipiell heikel, um Flächen plastisch darzustellen, und zudem sticht es leicht ins Matte oder gelbliche. Die Lichter und Reflexionen müssen lange erprobt werden. Man beacht hier den leichten blauen Schlagschatten, der ein bisschen die räumliche Wirkung verstärkt.

Formel
- x^2+y^2+z^2+1500\cdot(x^2+y^2)\cdot(x^2+z^2)\cdot(y^2+z^2)-1=0
Distel (Thistle)
Die Fläche Distel mit der Gleichung x2+y2+z2+c(x2+y2)(x2+z2) (y2+z2) = 1 besticht durch ihr hohes Maß an Symmetrie. Für das tatsächliche Bild wurde der Koeffizient c sehr groß gewählt. Die sechs Zacken befinden sich auf den drei Koordinatenachsen des euklidischen Raumes. Jede Drehung, die die drei Achsen in sich selbst überführt, lässt auch Distel unverändert. Die Symmetriegruppe ist also die des Würfels und des zu ihm dualen Oktaeders, zwei der fünf platonischen Körper.
Es ist schon erstaunlich, dass es nicht möglich ist, vollkommen regelmäßige Sterne wie Distel mit beliebig vielen Zacken zu konstruieren. Dies folgt aus Überlegungen der Gruppentheorie. Es sind nur vier, sechs, acht, zwölf oder zwanzig Spitzen möglich, gemäß der Anzahl der Seiten der platonischen Körper. Wir überlassen es dem neugierigen Betrachter, für all diese Sterne die passenden Gleichungen zu finden.
Dullo
Schreien im Oval einer modernen Fußballarena die Zuschauer bei einem Tor (üblicherweise der eigenen Mannschaft), so breitet sich der Schall wie ein Schwimmreifen aus, den man rasch aufbläst. Nach einigen Sekundenbruchteilen berührt sich der Schwimmreifen innen - die Öffnung hat sich geschlossen - und das passiert genau am Anstoßpunkt. Dort treffen alle Schallwellen gleichzeitig von allen Richtungen ein und verstärken sich entsprechend. Darum werden Schiedsrichter angewiesen, immer auf Ballhöhe zu sein. Dies soll verhindern, dass sie bei „Tor” im Mittelkreis stehen und Ohrensausen bekommen.
Eistüte (Cone)
Der horizontale Schnitt von Eistüte ist eine so genannte Rosettenkurve: Ein kleines Rad rollt im Inneren eines Kreisringes ab. Ein auf dem Rad befestigter Bleistift zeichnet dabei eine Kurve. Je nach dem Verhältnis der beiden Radien bilden sich verschiedene Kurven. Die Kurve schließt sich genau dann, wenn das Verhältnis eine Bruchzahl ist. In unserem Fall ist es der Vierklee.
Unsere Eistüte hat den Vorteil, dass vier Kugeln draufpassen. Man muss sie schnell schlecken, sonst tropft das Eis innen durch.
Helix
Die Lemniskate ist die ebene Kurve mit der Gleichung y4+z2 = y2. Diese ergibt sich aus dem Kreis y2+z2 = 1, indem man z durch z/y ersetzt. Geometrisch entspricht die Substitution der einmaligen Verwindung des Kreises zur Achterschleife. Fasst man y4+z2 = y2 als Gleichung in den drei Variablen x, y und z auf (wobei x blinder Passagier ist), so ist die Lösungsmenge eine Fläche im dreidimensionalen Raum, nämlich der Zylinder über der Lemniskate. Die Gleichung y4+x2z2 = y2 von Helix erhält man nun, indem z durch xz ersetzt wird. Geometrisch gesehen ist diese Konstruktion eine Art Faltung. Die Symmetrie bezüglich x und z ist klar erkennbar. Für die endgültige Formel wurden noch die Faktoren 2 und 6 dazu genommen, um Helix etwas zu strecken. Der singuläre Ort ist ein Kreuz von Geraden. Die Schnitte von Helix mit den Ebenen x = c oder z = c sind für c ≠ 0 Lemniskaten, die Schnitte y = c sind hingegen Hyperbelpaare.
Herz (Heart)
Trotz der einfachen Gleichung y2+z3 = z4+x2z2 besitzt die Fläche Herz eine subtile lokale und globale Struktur. Der singuläre Ort ist eine Gerade, längs der sich die Fläche selbst schneidet. Der Ursprung 0 ist der interessante Punkt: Wir schneiden Herz mit Ebenen x = c orthogonal zur singulären Geraden. Es entsteht eine Schleife, die sich wie ein Knoten zusammenzieht, wenn c gegen 0 strebt. Dadurch kommt es zur Trichterbildung. Von der Ferne betrachtet sehen wir eine kreisförmige Öffnung in der Fläche. Der Schnitt mit der vertikalen xy-Ebene ist in der Tat ein Kreis. Die Schlichtheit der Fläche bedingt, dass wir ihre Gestalt erfassen und uns merken können. Mit geschlossenen Augen vergegenwärtigen wir uns sofort die Figur in jedem Detail. Viel schwieriger ist es, die geometrischen Verhältnisse mit Worten einem Dritten mitzuteilen. Die geeignete Sprache fehlt.
Himmel & Hölle (Heaven and Hell)
Ein Blatt Papier wird gefaltet und dann so von unten gehalten, dass man vier Finger in die vier entstandenen Ecken stecken kann. Durch Spreizen der Finger öffnet sich die Form auf zwei verschiedene Arten, man sieht jeweils zwei der vier inneren Seiten, die blauen für den Himmel, die roten für die Hölle. Die Kinder raten, welche Farbe erscheinen wird. Unsere Figur erinnert ein bisschen an dieses Spiel, daher der Name.
Die Quadrate bei y und z werden zueinander addiert, das ergibt die höchste vorkommende Hochzahl 4. Man spricht von einer Gleichung vom Grad 4. Je höher der Grad, desto komplizierter ist es, die Fläche zu berechnen.
Kolibri (Hummingbird)
Wie man sich leicht überzeugt, ist Kolibri eine auf den Kopf gestellte Nahaufnahme von Herz in der Nähe des Ursprungs. Die Gleichung ist x3+x2z2 = y2, man vergleiche mit der Formel y2+z3 = z4+x2z2 von Herz. Ersetzt man in letzterer x durch z und z durch −x, läßt sich das Monom x4 durch einen Koordinatenwechsel eliminieren, sodass die Gleichung von Kolibri resultiert. Der Kolibri ist als einer der kleinsten Vögel mit beeindruckenden Fähigkeiten ausgestattet. Seine Flügel vermögen bis zu 200 mal pro Sekunde zu schlagen, sodass er in der Luft still stehen bleiben kann. Diese Aktivität verbraucht sehr viel Energie, der Kolibri muss daher täglich das Doppelte seines Körpergewichts an Nahrung aufnehmen. Ohne ständige Kalorienzufuhr würde er innerhalb weniger Stunden verhungern. In der nächtlichen Ruhephase senkt er seine Körpertemperatur wesentlich, um an Energie zu sparen.
Kreisel (Spinning Top)
Die Gestalt des Kreisels als Lösungsmenge einer einfachen algebraischen Gleichung darzustellen ist eine kleine mathematische Bastelei. Es ist auch mathematisch nicht sofort einsichtig, wie diese Gleichung auszusehen hat, abgesehen davon, dass sie nicht eindeutig sein muss: Verschiedene Gleichungen können ähnliche Formen liefern. Im Bild wurde die Gleichung 60(x2+y2)z4 = (60−x2−y2−z2)3 gewählt. Die Rotationssymmetrie um die vertikale z-Achse erkennt man am Auftreten von x und y im quadratischen Polynom x2+y2. Die dritte Potenz auf der rechten Seite ist notwendig, um die beiden Spitzen zu erzeugen. Und da z nur mit geraden Potenzen vorkommt, ist die Fläche symmetrisch bezüglich der Spiegelung an der horizontalen xy Ebene. Der zweimalige Parameter 60 zur Balance der Proportionen hat ästhetische Gründe.
Miau
Diese Fläche wurde durch Probieren auf einer eher eintönigen Zugfahrt gefunden (Arbeiten mit algebraischer Visualisierung lässt die Zeit sehr schnell vergehen). Die Konstellation ist aber keineswegs zufällig - im Gegenteil, wollte man für diese Fläche die algebraische Gleichung systematisch herleiten, stieße man wohl auf unüberwindbare Probleme. Der Reiz von Miau ist natürlich die doppelte Öffnung mit eingelagerter Singularität. Für den Mathematiker ist dies eine Fundgrube, die geheimnisvolle Beziehung zwischen Gleichung und Form zu erforschen.
Nepali
Wir betrachten die definierende Gleichung (xy−z3−1)2 = (1−x2−y2)3 von Nepali. Die Symmetrie zwischen x und y wird verstärkt durch das quadratische Polynom x2+y2, das rotationssymmetrisch ist, im Gegensatz zum Monom xy. Schnitte mit den horizontalen Ebenen z = c liefern geschlossene Kurven, die annähernd Kreise sind. Das gleichzeitige Auftreten von Quadraten und dritten Potenzen bewirkt das spitze Zulaufen am Gipfel. Die seitliche Berandungskurve von Nepali ist kein exakter Kreis, sondern wölbt sich auf und ab wie die Krempe eines Hutes. Ihre Projektion auf die horizontale xy-Ebene ist indessen ein Kreis, wie man an der Draufsicht erkennt. Die gezeigte Fläche ist beschränkt, sie musste also nicht mit einem Würfel oder einer Kugel geschnitten werden. Diese Tatsache ist aus der Formel durch eine sorgfältige Analyse direkt herleitbar.
Seepferdchen (Seahorse)
Wollte man die Gleichung für diese Fläche finden, müsste man sich ordentlich anstrengen. Denn die zarte Berührung ist nicht leicht zu erreichen. Ändert man nur ein bisschen die Formel, schon ist die Berührung verschwunden. Die Eleganz des Seepferdchens täuscht. Schaut man von hinten oder von der Seite darauf, wirkt es recht plump - aber das kommt ja bei anderen Lebewesen auch manchmal vor. Seepferdchen leben weltweit in tropischen und gemäßigten Meeren. Sein lateinischer Name ist Hippocampus, seine Formel steht daneben.
Solitude
An der Gleichung x2yz+xy2+y3+y3z = x2z2 von Solitude lässt sich die versteckte geometrische Vielfalt nicht erkennen. Ebenso zeigt das Bild nur einen Teil der Phänomene. Aufschlussreich ist hingegen eine Kamerafahrt rund um die Fläche, wie sie im Film „ZEROSET – I spy with my little eye” zu erleben ist. Offensichtlich gibt es zwei Öffnungen, eine größere, gut sichtbare, sowie eine kleinere, die man bei der ersten Perspektive nicht vermuten würde. Der Blick von oben zeigt die vertikale singuläre Gerade, längs der horizontale Schnitte eine spitze Kurve erzwingen. Am Beispiel von Solitude erkennt man die Komplexität des Problems, aus der Gleichung die sichtbare reelle Geometrie zu deduzieren. In ähnlicher Weise kann man die zugrundeliegende komplexe oder zahlentheoretische Geometrie hinterfragen.
Tanz (Dance)
Die Gleichung 2x4 = x2 +y2z2 von Tanz liefert bei Einsetzen von z = 0 die Gleichung 2x4 = x2. Dies ist der Schnitt von Tanz mit der horizontalen xy-Ebene. Umschreiben ergibt die Gleichung x2(√x+1)(√x-1) = 0 von drei parallelen Geraden. Wir beobachten hier ein typisch reelles Phanomen: Die Gerade x = z = 0 gehort zur Losungsmenge der Gleichung 2x4 = x2+y2z2 von Tanz, ist aber eine isolierte, eindimensionale Komponente. Denn fur x nahe 0 gibt es nur die Losungen x = y = 0 oder x = z = 0, also das Achsenkreuz bestehend aus der y- und z-Achse. Geraden sind unendlich dunn. Sie werden daher vom Visualisierungsprogramm ubersehen, bzw. nicht eingezeichnet. Man muss also die Existenz von eindimensionalen Komponenten in der Losungsmenge vorher rechnerisch abklaren und sie dann gegebenenfalls als dunne Zylinder in das Bild einfugen.
Taube (Dove)
Für Taube lautet die erstaunliche Formel 256z3 − 128x2z2+16x4z +144xy2z−4x3y2−27y4 = 0. Die Koeffizienten sind nicht zufällig. Im Gegenteil: Die Gleichung folgt aus einer anderen, allgemeineren Formel ab, der sogenannten Diskriminante. Diese beschreibt den Schatten einer Fläche oder Varietät, der bei der Projektion auf eine Ebene oder einen höher dimensionalen linearen Raum entsteht.
Die Kontur ist durch die Fläche und die Projektion eindeutig festgelegt, und, algebraisch gesehen, auch die Gestalt ihrer Gleichung.
Tülle (Nozzle)
Die Fläche Tülle konstituiert sich aus drei glatten Komponenten, die sich jeweils paarweise in einer (ebenfalls) glatten, ebenen Kurve schneiden. So erhält man drei Schnittkurven, und zwar eine Gerade und zwei Parabeln. Man beachte, dass diese Kurven sich tangential in 0 berühren. Wir haben hier das einfachste Beispiel einer Fläche mit drei paarweise transversalen Komponenten, sodass sich die Schnittkurven von je zweien nicht transversal schneiden. Die Fläche ist damit keine Mikado-Varietät. Der transversale Schnitt von zwei glatten Komponenten einer Fläche – ein grundlegendes Konzept der Geometrie – lässt sich algebraisch präzise durch die sogenannte Idealtheorie in Formeln fassen. Mit ihr kann man ausgezeichnet rechnen und Beweise führen. Für singuläre Komponenten ist die richtige, der Anschauung entsprechende Definition von Transversalität noch ausständig.
Zeck (Tick)
Die einfache Gleichung x2+y2 = z3(1−z) von Zeck bestimmt, wie bei den anderen Flächen, vollkommen die Geometrie. Das heißt, sowohl die singulären Punkte wie auch die äußere Gestalt, die Krümmung und die Ausdehnung werden durch die vier Monome x2, y2, −z3 und z4 eindeutig festgelegt. Damit ist die Formel ein sehr effizienter Code, um kompliziert aussehende Formen zu chiffrieren. Allerdings ist die geometrische Information nicht immer schnell aus der Formel ablesbar. Die lokale Gestalt der Fläche in der Nähe eines gegebenen Punktes lässt sich meistens explizit bestimmen, die Techniken der lokalen analytischen Geometrie greifen gut. Die Feststellung der globalen Struktur erfordert wesentlich mehr Aufwand und kann nicht immer befriedigend durchgeführt werden.