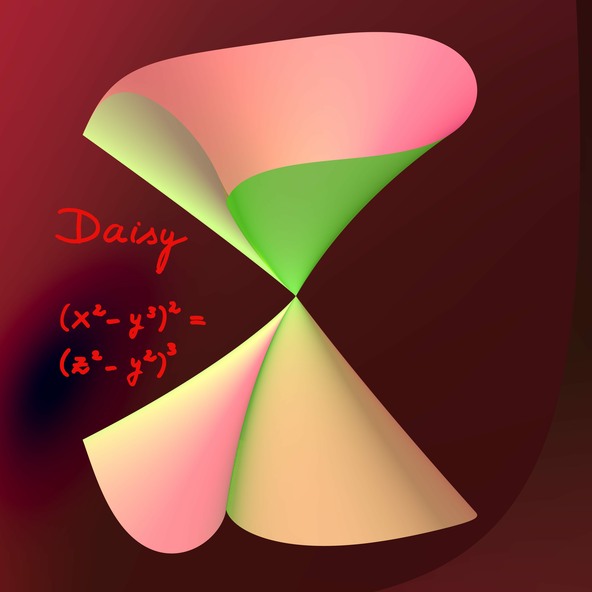Maths can be beautiful! On June 6th at 11 am, two new interactive stations will be presented at the EXPERIMINTA ScienceCenter in Frankfurt, Germany. At the opening Prof. Oldenburg, Goethe-Universität in Frankfurt, and Dr. Matt, Mathematisches Forschungsinstitut, Oberwolfach will be present. The two stations are accompanied by a gallery of beautiful visualizations and will be permanently displayed at the science center.
Herwig Hauser clásico
Con motivo de la exposición original IMAGINARY, se recopilaron las superficies algebraicas clásicas de Herwig Hauser. El motivo por el que se escogieron las fórmulas y formas de Herwig Hauser es porque ecuaciones resultan simples y bonitas. Las figuras son sencillas y naturales y muestran información geométrica interesante. Herwig Hauser es profesor de matemáticas en la Universidad de Viena y trabaja en geometría algebraica y teoría de singularidades.
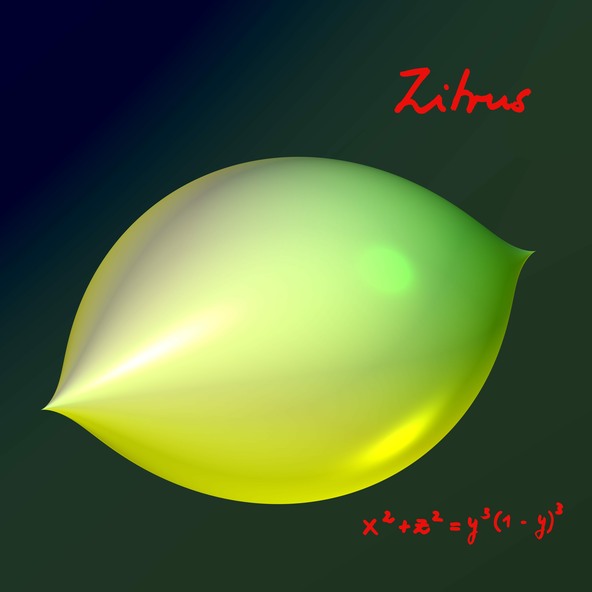
Zitrus (Limón)
Esto no es un limón / La traición de las imágenes
Al ver esta imagen, seguramente todos hemos pensado: “Esto es un limón”. Pero si es un limón, ¿Por qué no tiene olor ni sabor? ¿Por qué no tiene ni poros ni manchas? ¡Está claro que esto no puede ser un limón!
En efecto, esta figura no es un limón, sino un modelo matemático de un limón, que nos ayuda a entender mejor las propiedades de la forma que tiene el limón. Las ecuaciones nos permiten construir modelos matemáticos que se parecen a las cosas, y estudiar estos modelos matemáticos nos ayuda, a su vez, a entender mejor la forma de las cosas.
«El mapa no es el territorio»
Alfred H. S. Korzybski
Todo esto forma parte de la “poesía” de las Matemáticas. A partir de ecuaciones algebraicas podemos generar bellas superficies que transportan nuestros pensamientos hasta rincones insospechados de nuestra mente.
Limao (Lima)
En el punto de equilibrio / El egocentrismo de las figuras
Una figura tiene simetría central cuando todos sus puntos están dispuestos regularmente respecto de un punto, llamado centro de simetría: cada punto tiene un punto simétrico en la figura a igual distancia del centro, en la misma dirección pero en sentido opuesto.
En Lima puedes detectar fácilmente cuál es su centro de simetría. Aunque en este caso el centro pertenece a la figura, no siempre es así. Si el centro es el origen de coordenadas, la simetría central se descubre fácilmente en la ecuación: sustituyendo (x,y,z) por (-x,-y,-z) nos da la misma ecuación.
El concepto de simetría central hace referencia a orden, equilibrio y a que hay un único punto que coordina a todos los demás. Es por ello que muchas veces se utiliza para simbolizar el origen de la vida, el centro de gravedad o depositario de la energía, quién es el dueño de un conjunto de cosas, etc. Ejemplos de estas connotaciones los puedes encontrar en muchos símbolos religiosos.
Vis à Vis (Tú y Yo)
Singular versus liso / Amigos o enemigos
Los puntos singulares, o singularidades, a menudo se identifican fácilmente de forma visual porque son puntos donde la superficie no es lisa ni suave, como por ejemplo un pico o un pliegue.
La superficie Tú y Yo ilustra muy bien lo que es una singularidad, el pico de la izquierda, y lo que no lo es, la colina lisa de la derecha. Las singularidades son interesantes entre otras cosas porque, al contrario de lo que ocurre con los puntos lisos que son estables, pequeños cambios en la ecuación pueden cambiar su aspecto de un modo sorprendente.
¿Sabes que hay gente que se dedica especialmente al estudio de estos puntos? Los agujeros negros y el principio del universo, Big Bang, son singularidades de las ecuaciones de los modelos cosmológicos. Sin ir más lejos, ¡las singularidades de nuestras huellas dactilares nos identifican!
Calypso (Calipso)
La estética de la inestabilidad / Ecuaciones de la creatividad
Las singularidades son delicadas o inestables, como Calipso. Pequeñas modificaciones en su ecuación transforman la superficie radicalmente.
La inestabilidad de las singularidades es la esencia de su belleza. Esto también ocurre en arquitectura, por ejemplo con las superficies plegables: su inestabilidad permite el movimiento de la estructura y así cambiar su forma.
¿Sabías que los arquitectos usan ecuaciones para saber qué forma va a presentar su obra en cada momento durante el despliegue? Los grandes arquitectos son también grandes conocedores de las Matemáticas, y las ecuaciones les permiten experimentar con las formas soñadas.
«El plegado, como un medio para cambiar la forma de un armazón, contradice el principio de estabilidad en tanto que esta última es la capacidad de retener la forma. Así, una estructura plegable debe necesariamente ser inestable.»
Olga Gil Medrano, Un mundo en el bolsillo, la geometría plegable de Santiago Calatrava.
Calyx (Cálix)
Elevarse a dimensiones superiores / Atrapadas en la caverna de las sombras
Los puntos singulares de Cálix son todos los del eje y. Si explotamos esta recta, como hicimos con el punto singular de Cruasán, obtenemos un cilindro, y ¡Cálix se transforma en Calipso! Si vuelves a contemplar a Calipso no verás este cilindro porque habita en dimensiones superiores, y sólo comparte con Calipso y su mundo tridimensional una recta.
Otra manera de entender esto es imaginando el proceso inverso: mediante una proyección adecuada en un espacio 5-dimensional la superficie del cilindro se contrae a la recta singular de Cálix, y de este modo ¡Cálix es la sombra de Calipso!
Un resultado sorprendente del matemático Heisuke Hironaka afirma que cualquier superficie con alguna singularidad es la sombra de alguna superficie lisa, es decir, sin singularidades, que puede habitar en un espacio de dimensión superior a tres.
Podemos imaginar que el mundo tridimensional es una caverna que atrapa las sombras de realidades de dimensión superior…
Daisy (Campanilla)
Con ojo matemático / Reconocer las singularidades
Has aprendido que puntas y pliegues son singularidades, aunque hay más tipos. Pero imagina ahora que te tapan los ojos y te impiden tocar la superficie. ¿Cómo podrías encontrar sus singularidades?
Las singularidades se definen como todos aquellos puntos de la superficie que son solución de las derivadas parciales de su ecuación. Este método permite encontrar las singularidades con papel y lápiz, sin ni siquiera tener cerca la superficie, tan sólo mediante su ecuación.
Por ejemplo, derivando la ecuación x2 + y2 − z2 = 0, que representa un cono, respecto de x, obtenemos 2x; respecto de y, 2y; y respecto de z, −2z. Estas tres derivadas se anulan a la vez sólo en el punto (0,0,0). Como (0,0,0) es un punto del cono, hemos encontrado el único punto singular del cono, que, como podíamos esperar, ¡es la punta del cono!
Si sigues este método con Campanilla, encontrarás que sus puntos singulares forman dos curvas planas que se cortan transversalmente en su punto singular común.
Diabolo
La revolución de la revolución / Las superficies del alfarero
La porción de la derecha de Diábolo es simétrica de la porción izquierda. Además parece que cada una de ellas se haya obtenido usando un torno de cerámica, haciendo girar una curva parabólica. Las superficies que se obtienen haciendo girar una curva se llaman superficies de revolución, y la curva que hemos hecho girar se llama generatriz.
Es lo que le ocurre al volcán Rangitoto, que se encuentra en Auckland, Nueva Zelanda, a unos 19000 km de aquí: por muchas vueltas que des a su alrededor, el paisaje te parecerá siempre igual.
«Conozco Rangitoto. La gente de Auckland se volvía para verlo, señalarlo y decir: Tiene una forma peculiar; sea cual sea el ángulo desde el que se mire es igual; es el lugar más emblemático de Auckland, su fenómeno. Lo observaban y observaban, pero no lo conocían, y Grace no lo conocía, aunque si había aprendido a asignarle atributos poéticos; su uniformidad exterior oculta una sorpresa interior.»
Janet Frame, Hacia otro verano.
Cada una de las dos superficies que forman Diábolo oculta una sorpresa interior: es un espejo parabólico y los reflejos los rayos de luz paralelos al eje de revolución se cortan en un punto.
Ding-dong (Lágrima)
Deformar la figura deformando la ecuación / El equilibrio de las estalactitas
La ecuación y la forma de Lágrima son muy simples. La figura se ha obtenido girando la forma de la letra griega alfa alrededor de un eje. Mirándola al revés parece una gota de agua. ¡Casi se podría decir que la vemos caer!
Añadiendo parámetros a su ecuación, y modificándolos de manera continua, podemos crear una secuencia de imágenes en las que podríamos ver cómo se genera la gota, cómo se va acercando a su posición límite, y cómo finalmente se desprende. Es como crear una secuencia de fotogramas de una película.
En cada instante, la gota está en una situación de equilibrio, donde la fuerza de la gravedad compensa la tensión superficial del líquido. Pero el equilibrio de Lágrima es claramente inestable, y las gotas pasan por él temblando hasta desprenderse. La Teoría de Catástrofes del matemático René Thom estudia como pequeños cambios de los parámetros pueden llevar a súbitos cambios de equilibrio.

Fórmula
- x^2+y^2+z^2+1500\cdot(x^2+y^2)\cdot(x^2+z^2)\cdot(y^2+z^2)-1=0
Distel (Destello)
¿Formas caprichosas? / Encajes singulares
La imagen en blanco y negro parece una fotografía de Destello, pero en realidad es la de un virus. Los virus utilizan sus pinchos, sus singularidades, a modo de llaves para entrar en las células, en donde pueden dividirse y crecer.
Una figura es simétrica si existe una transformación que la deja igual. Las simetrías de una figura se pueden reconocer a través de su ecuación. En Destello, por ejemplo, cualquier permutación de las variables de su ecuación da la misma ecuación y por eso tiene el mismo aspecto sea cual sea la punta que tenemos enfrente.
Estudiando las simetrías de los azulejos, los matemáticos demostraron que sólo hay 17 maneras de recubrir una superficie plana con baldosas. Todas ellas ya se encuentran en los muros de la Alhambra de Granada. Este mismo tipo de investigaciones en tres dimensiones permiten clasificar los cristales y las moléculas.
Dullo (Manzana)
Fenómenos singulares en la naturaleza / Comprender las singularidades para planificar
Las Matemáticas están muy estrechamente relacionadas con otros campos del conocimiento como la Física, la Química o la Tecnología. Proporcionan potentes herramientas para entender el mundo que nos rodea.
Muchos fenómenos que nos encontramos al estudiar la naturaleza dan lugar a modelos con singularidades, y conocerlas ayuda a evitarlas o a planificar estrategias para atravesarlas. Así ocurre con el diseño y funcionamiento de robots.
Otro ejemplo es la propagación de las ondas de sonido producidas por la ovación del público en un estadio, que toma la forma de la superficie Manzana, con una singularidad en su centro. Por esta razón y para proteger sus oídos, el árbitro de fútbol evita estar en el centro del campo cuando se celebra un gol.
Eistüte (Cucurucho)
Seccionar para investigar… / Cortes desveladores
Cuando queremos investigar un objeto, a menudo lo cortamos por la mitad. Una manzana entera tiene una forma redonda y un color rojizo, verde o amarillo, pero si queremos saber qué forma tienen sus semillas y de qué color es por dentro, tendremos que cortarla para descubrir su interior.
Si quieres estudiar una figura también la puedes cortar y observar qué información aportan las curvas que obtienes. Por ejemplo, al cortar una esfera por cualquier plano obtienes una circunferencia. Esta acción de “cortar” se denomina seccionar.
La misma técnica utilizan los médicos para hacer tomografías, seccionando el cerebro por planos paralelos.
Fíjate que la sección superior de Cucurucho es en forma de flor. Y dada su semejanza con un cucurucho, si pones una bola de helado encima de ella, ¿cómo puedes saber si el helado derretido lo atravesará y caerán gotas por abajo? Seccionando…
Helix (Hélice)
Más finas que una pompa de jabón / No se pueden esculpir de lo finas que son
Las pompas de jabón son extremadamente delicadas, tanto que a veces parece que estallen por el simple hecho de mirarlas.
Sin embargo, su superficie está formada por una capa de agua atrapada entre dos capas de jabón. Cuando son demasiado finas, por ejemplo cuando la pompa de jabón crece, el agua de la capa interior hace estallar la burbuja.
Las superficies algebraicas son muchísimo más finas que las pompas de jabón, ya que están hechas de una sola capa de puntos. Y como sólo usamos nuestra imaginación para producir los puntos, sin grosor ni masa, las superficies no estallan, aunque tengan puntas o pliegues tan marcados como los de Hélice.
Así, si queremos tocar la superficie de Hélice en un modelo tridimensional, tenemos que crear una escultura más gruesa de lo que es Hélice en realidad, engrosando la superficie por uno de los lados. La escultura de Hélice que se muestra en la vitrina se ha engrosado por su lado interior.
Herz (Corazón)
Mirar los árboles sin dejar de ver el bosque / Estudio local y global de las superficies
¿Has visto el pingüino y el tulipán que algunos visitantes como tú han dibujado con SURFER? Para conseguirlo, han tenido que multiplicar varias ecuaciones, ya que determinar todos los detalles de una superficie algebraica con solo una ecuación, como en Corazón, es muy difícil. La unión de lo “local”, el detalle, de todos los puntos forma lo “global”, la forma, de la superficie.
Aspectos globales de una superficie son por ejemplo su grado, el tipo de curvas de sus secciones, o saber como está construida. Este es el caso del Teorema Egregium de Gauss, que afirma que no se puede construir una esfera con una hoja de papel sin tener que arrugarla o rasgarla.
En cambio, aspectos locales de una superficie son por ejemplo saber si hay una singularidad en un punto o si el contacto de una superficie con otra alrededor de un punto es intenso o más bien superficial.
Himmel und Hölle (Comecocos)
Creando nuevas formas / La simplicidad asombrosa del Álgebra
Para crear nuevas formas es preciso conocer las ecuaciones. Sus piezas básicas son los monomios, expresiones algebraicas con letras y números. Del monomio se distinguen los elementos siguientes:
signo, coeficiente, variables, exponentes y grado.
Por ejemplo:
2xy2z = +2x1y2z1
El grado del monomio es la suma de los exponentes de las variables que lo componen:
grado = 1+2+1 = 4
Para formar ecuaciones sólo se usan las operaciones de suma, resta y multiplicación, que conocemos desde que somos muy pequeños. Y sin embargo, con operaciones tan simples se consigue obtener superficies muy especiales: las superficies algebraicas.
¿Te atreves a crear formas con puntas o agujeros solamente sumando y multiplicando?
Kolibri (Hummingbird)
Diálogo entre Geometría y Álgebra / La ecuación es el jefe de los puntos
Esto es lo que nos dice el Álgebra sobre Colibrí: está formada por todas las ternas (x, y, z) de números que cumplen x2= y2z2+z3. Por ejemplo,
(0,0,0), (1,0,1) y (3,–2,–3)
son puntos de Colibrí, mientras que (0,1,1) no lo es.
En general, la ecuación describe exactamente la figura: a cada punto le corresponde una terna de números (x, y, z) que es solución de la ecuación y viceversa.
Pero, ¡Colibrí es una figura geométrica que vemos en el espacio! ¿Cómo sale la figura de Colibrí a partir de estos números?
Esto nos lo dice la Geometría: para interpretar x, y, z necesitas elegir un convenio para orientarte en el espacio, esto es, un sistema de coordenadas. Éste consta de tres ejes que pasan por un punto, llamado origen, y que determinan las tres direcciones atrás-delante, derecha-izquierda y abajo-arriba. Así, las coordenadas (x, y, z) indican cuánto se ha recorrido en cada una de las tres direcciones desde el origen hasta llegar al punto en cuestión.
Kreisel (Giroscopio)
A través del espejo / Mi otro yo
Una de las simetrías más usadas en el mundo literario y místico es la especular. El nombre hace referencia a los reflejos, por ejemplo en un lago o en un espejo.
Un ejemplo de ella es Giroscopio. Si debajo de la parte verde hubiera un lago, la parte azul parecería su reflejo. ¡Así es como funciona la simetría especular! Fíjate que en su ecuación la variable z solo aparece con exponentes pares.
Para muchos autores, esta simetría ha inspirado un mundo donde izquierda es derecha, los niños son adultos y la gente rejuvenece.
Esta idea viene de la propiedad matemática de la simetría especular de invertir la orientación. Esto nos lo explica la conversación entre el escritor L. Carroll, autor de “Alicia a través del espejo”, y una niña, Alice:
«-Primero quiero que me digas en qué mano tienes la naranja.
-En la derecha -contestó Alice.
-Ahora -dijo Carroll- fíjate en el espejo y dime en qué mano tiene la naranja la niña que ves en él.
-En la izquierda -dijo Alice.
-¿Y cómo se explica eso? -le preguntó Carroll.
La niña se quedó dudando, pero al fin dijo:
-Si yo estuviera al otro lado del espejo, ¿no es cierto que la naranja seguiría estando en mi mano derecha?
-¡Bravo, mi pequeña Alice! -exclamó Carroll- ¡Es la mejor respuesta que he recibido hasta el momento!»
Stuart Dodgson Collingwood, La vida y cartas de Lewis Carroll
Miau
Tantas superficies como agujeros / Están vacíos pero son importantes
En Miau hay un enorme agujero doble en el centro, a través del cual vemos una de sus singularidades. Puede parecer que los agujeros, al estar vacíos, no tienen ninguna importancia, pero de hecho nos ayudan a conocer mejor la superficie.
En el caso de superficies lisas acotadas y de una sola pieza, el número de agujeros, como el del donut, incluso las clasifica. Esto es así en el ámbito de la Topología, donde se permite deformar elásticamente la superficie, pero no rasgarla, pegarla o estrangularla. Así, ¡la superficie de una taza de café es la misma que la de una rosquilla!
Los agujeros también tienen no menos importancia en otras ocasiones. Según hayan o no burbujas –agujeros– en la cámara magmática de un volcán, su erupción podrá ser explosiva o solo efusiva. Lo mismo ocurre con las burbujas de gas que liberan las bacterias de la fermentación del queso Emmental: acaban produciendo un queso lleno de agujeros.
Nepali (Nepalí)
¿Caben en una bola o se extienden hasta el infinito? / Un mundo sin fin
Quizás alguna superficie te parezca francamente hermosa y tengas ganas de meterla en una bola de cristal llena de nieve, para poderla agitar y jugar con ella. Pero ¡no vayas a creer que puedes elegir cualquier superficie y meterla en tu habitación!
Hay superficies que se extienden hasta el infinito y, por muy bonitas que sean, jamás las podrás meter dentro de una bola de cristal, aunque sea inmensa. Si esto ocurre, se dice que no son acotadas y para dibujarlas hemos de escoger una porción: por eso parece que algunas estén cortadas, como Embrollo, de la cual sólo vemos la porción contenida en una esfera. En cambio Nepalí está acotada. ¿Te atreves a deducirlo de su ecuación?
La propiedad de ser acotada no es fácil de percibir empíricamente, incluso con la ayuda de SURFER. Es como el averiguar si el universo está acotado; aunque no conozcas sus límites, puede ser que los tenga o que no.
Seepferdchen (Caballito de mar)
Singularidades delicadas / Contactos sutiles
La superficie Caballito de Mar se repliega y se autointerseca en un único punto, que es singular. El suave contacto tangencial entre las dos porciones es muy difícil de conseguir jugando con ecuaciones. Se trata de una singularidad muy delicada, y cualquier pequeña modificación de la ecuación destruye este contacto sutil. ¡Cambia su ecuación mediante SURFER y observa el resultado!
Quizás esta bonita superficie se llama así porque los caballitos de mar también son animales muy delicados. Sólo viven en praderas de posidonia y zonas arenosas.
Pero la delicadeza de esta singularidad quizás es más comparable a la de la mimosa púdica. Es una planta que no permite que la toquen sin cambiar de forma: si alguien intenta hacerlo, ella, a modo de protección, cierra sus hojas y se coloca en una posición en la que no permite que miren su interior.
Solitude
La ecuación de la soledad x2yz+xy2+y3+y3z = x2z2 no revela su diversidad geométrica oculta. De manera similar, la imagen muestra sólo parte de los fenómenos. Sin embargo, lo que es informativo, es el recorrido de la cámara alrededor de la superficie como puede experimentarse en la película “ZEROSET – I spy with my little eye”.
Obviamente hay dos aperturas, una más grande muy visible y una más pequeña, que no sospecharías desde la primera perspectiva. La vista desde arriba muestra la línea recta singular vertical a lo largo de la cual las secciones horizontales fuerzan una curva pronunciada. El ejemplo de Soledad (Solitude) muestra la complejidad del problema para deducir la geometría real visible a partir de la ecuación. De manera similar, uno puede cuestionar el complejo subyacente o teoría geométrica de números.
Tanz (Danza)
Recta que te quiero recta / Superficies regladas
Las superficies regladas son las que se pueden generar mediante el movimiento de una recta que sigue un recorrido determinado.
Aunque Danza no es reglada, contiene rectas. Fíjate en dos de ellas que aparecen en la figura aisladas del resto: los ejes y, z. El programa SURFER no permite visualizar rectas o curvas aisladas. Para ver la curva dada por f=0 y g=0, se considera la ecuación f2+g2=0, que tiene las mismas soluciones reales, y se engorda a un fino tubo modificando un poco la ecuación, f2 + g2 – a = 0, para un valor pequeño de a.
Muchos arquitectos e ingenieros deciden trabajar con superficies regladas, no solamente por su diseño, sino también por las ventajas de su construcción: proporcionan rigidez y facilitan el uso del hormigón.
«Para que un objeto sea altamente bello es preciso que su forma no tenga nada de superfluo, solamente las condiciones materiales que lo hacen útil; se debe tener en cuenta el material de que se dispone y los usos que debe prestar; y de aquí nacerá la forma general. Cuando las formas son más perfectas exigen menos ornamentación.»
Antoni Gaudí
Taube (Pajarita)
Origami multidimensional / La ubicuidad de las cúspides
Si se nos cae un mantel al suelo, queda lleno de pliegues. La caída determina una asignación, o proyección, de los puntos del mantel en los del suelo, y los puntos de los pliegues forman una curva llamada discriminante.
La manera de saber si un punto es del discriminante, es decir, de un pliegue, es atravesando con un alfiler el mantel alrededor del punto: si el número de capas atravesadas no es el mismo en un entorno pequeño del punto, podemos asegurar que está sobre un pliegue.
Hassler Whitney observó que, en general, hay dos tipos de puntos en un pliegue: los que componen la curva del pliegue y su punto extremo. Estos puntos extremos se llaman cúspides.
Imagina que, en vez de superficies, manipulas objetos algebraicos de dimensión superior y que puedes hacer proyecciones entre ellos. Entonces el discriminante, o los pliegues, ya no serían curvas sino superficies o variedades de dimensión superior. Así es como aparece la figura de Taube: es una superficie discriminante.
Tülle (Embrollo)
Infinitos puntos en una palabra / Los “Pulgarcitos” de las Matemáticas
Del mismo modo que los impresionistas pintaban casas y prados con miles de puntos de pintura, las superficies también están formadas por miles de puntos. De hecho, una infinidad, ¡todos soluciones de una ecuación!
Una manera de pensar en el infinito es empezar a contar
1, 2, 3, …
Siempre hay un número mayor, y no acabamos nunca de nombrar todos los números naturales.
Fíjate en la ecuación de Embrollo: los factores yz multiplican toda la ecuación. Por tanto todos los puntos de los planos z=0 (horizontal) e y=0 (vertical) forman parte de Tülle.
Pero no solamente figuras como Tülle, que contiene dos planos, están formadas por una infinidad de puntos. Un cuadrado, sin ir más lejos, también.
Parece imposible que infinitos puntos quepan en un cuadrado, que es una porción finita, ¿verdad? Piensa que los puntos son tan pequeños que se les considera sin dimensiones, y si pudiéramos dibujar realmente uno, no sería perceptible al ojo humano.
Zeck (Peonza)
La ecuación, un nombre inequívoco / Imagina un nombre para esta figura…
Todas las figuras que se muestran en la exposición tienen nombre. Si tuvieras que nombrarlas tú, ¿qué nombres hubieras escogido?
¿Qué nombre crees que habrá puesto otra persona? ¡Pregúntalo!
Pero, ¿podemos encontrar un modo de nombrar figuras que nunca lleve a confusión? En Matemáticas se ha resuelto nombrándolas por su ecuación.
Una sola ecuación determina toda la figura, todos sus puntos, todas sus curvas, incluso todos sus agujeros, todos sus pliegues y todas sus puntas. Sólo falta aprender a encontrarlos en la ecuación o saber dibujarla. Es como cuando te enseñan a escribir: una vez sabes escribir sin faltas una palabra, todo el mundo la entiende.
Además, las ecuaciones se escriben y se interpretan igual en todas partes, porque el lenguaje de las Matemáticas es universal, como las partituras musicales.