The Italian premiere of a large IMAGINARY exhibition
SURFER Gallery by Bianca Violet
These images were created using SURFER. They have been used in exhibitions, for logos and other kind of purposes.
A collection of short animations created with the SURFER software can be found here.
Roman Candy
The Real Projective Plane is the space of lines in real three-dimensional space (R3) passing through the origin. When the mathematician Jakob Steiner stayed in Rome, he thought of a mapping of the Real Projective Plane into R3. The resulting surface intersects itself. It is now called Roman Surface or Steiner Surface.
There is a triple point in the origin and each of the three coordinate planes is tangential to the surface. Apart from the origin, the segments along the coordinate axes are double points, which terminate in six pinch points.
In the picture you see a yellow Roman Surface surrounded by six parts of the Roman Surface, meeting at the pinchpoints, emphasizing the high degree of symmetry of the surface.
Logo IMAGINARY-AIMS
This is a screenshot of an animation originally created for the movie ‘Imagine a Secret’.
Elliptic curves have deep and beautiful properties. They are plane curves of the type y2 = x3 + a·x + b that have been studied since the XIX century. That equation in the affine plane corresponds to the homogeneous equation y2·z= x3 + a·x·z2 + b·z3, which describes in space a family of algebraic surfaces with two parameters a and b. The computational variation of these equations generates beautiful animations that stimulate our imagination and evoke our mathematical creativity.
Here, three of such algebraic surfaces are seen (red, green and yellow), each having slightly different parameter values. There is also a semi-transparent black sphere adding a bit of a mystery to the center of the image. The bright curve-like parts of the three colored surfaces are not included in the black sphere, however, there are still part of the sphere containing the visible space created by the SURFER program.
Watch an animation showing these surfaces here.
Slice of Boy
Imagine sewing the edge of a Möbius strip, which is just one closed curve, to the boundary of a disk! The resulting closed surface still contains the Möbius strip and will therefore be non-orientable (you cannot tell what is the outside or the inside - it is all the same). That is why it must have self-intersections in our real three-dimensional space. But can it be done smoothly with no sharp or pointy edges?
The famous mathematician David Hilbert assigned his student Werner Boy to prove that it is impossible. To the surprise of his teacher, Boy constructed such a smooth surface in 1901. He described it by giving the corresponding curves of its intersection with a family of parallel planes.
Now in this picture, you see a slice of two Boy surfaces (one being the mirror image of the other), cut not by planes but by two spheres with the same center and of slightly different radii.
The formula for such Boy surfaces is by François Apéry.
Logo IMAGINARY Israel
A pair of three-twisted Möbius strips.
The Möbius strip is a well-known classical object in geometry and topology which attracts not only professional mathematicians, but many people. It can be obtained by gluing a strip of paper with a twist. If the edges are twisted k times before gluing (with k being an odd integer), the k-twisted Möbius strip is obtained. If k were an even integer, the resulting surface would be a twisted cylinder surface.
A solid Möbius strip is defined as the boundary of a small smooth tubular neighborhood of a Möbius strip.
Find out more about how to create solid Möbius strips with the SURFER software here.
Clinch
The formula: x² y² + y² z² + x² z² + xyz = 0
describes a shape, which was discovered by Jakob Steiner. While he stayed in Rome in 1844, he studied its geometrical properties - hence it is called Roman surface. However, it was his friend Karl Weierstraß, who first published a paper on the surface and Steiner’s results in 1863, the year of Steiner’s death.
In the picture there are 18 Roman surfaces positioned symmetrically around the origin, each surface only slightly translated off the origin along one or two of the coordinate axes, so they intersect each other. Additionally, only a small portion of the whole arrangement is shown in this picture: everything within a small spherical neighborhood of the origin. Anything outside is simply cut off.
Even though the Roman surface is non-orientable, which means there is no outside or inside - just one side, the SURFER program assigns two colors to it. Here each surface has one bright first color, while the second color is black, which is also the background color.
NIMS-IMAGINARY logo for the ICM 2014
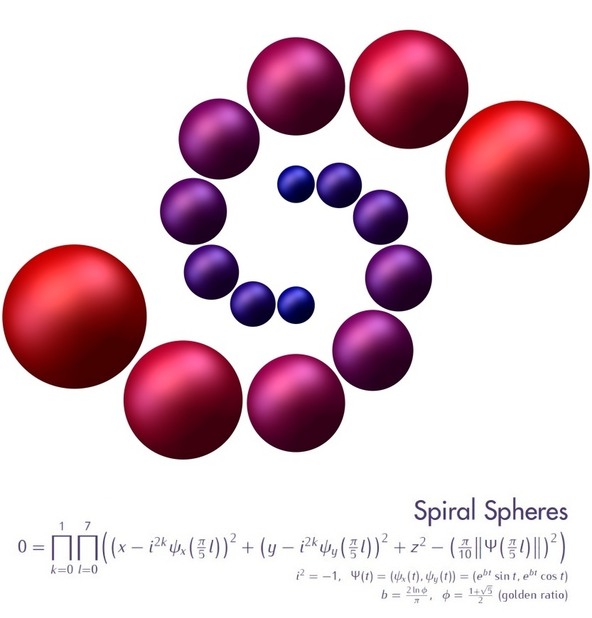
The logo for the NIMS-IMAGINARY exhibition at the ICM 2014 in Seoul, South Korea, was designed to be similar to the ICM logo, which represents growth with mathematical order, and symbolizes the dreams and hopes for the late starters. The S-shaped logo is reminiscent of the S in Seoul, and also the ‘Tae-Geuk’ image in the Korean flag. The Tae-Geuk symbolizes the harmony of Yin and Yang. The red color is Yang, love and passion. The blue color is Yin, intelligence and dream. The Yin and Yang, however, begin with the same color and shape, representing the oneness of the universe.
In the Spiral Spheres logo of the NIMS-IMAGINARY exhibition 16 spheres with their centers along two golden spirals (one spiral for k=0 and the other for k=1) are displayed. The function Psi is the parametric form of the spiral curve. The radius of each sphere is proportional to its distance to the origin, which is the length of the vector Psi.
Watch an animation of the Spiral Spheres here.
MaTiE logo
The logo for the project ‘Mathematics in Europe’ was created by combining two versions of the Togliatti Quintic, which is part of the gallery integrated in the SURFER software. The logo combines the European colors and resembles the five-pointed star. It symbolizes the connections and interrelations between the countries as well as the strong formation when working together.
Eugenio Giuseppe Togliatti proved in 1937, that there is a surface of degree 5 - a Quintic - with exactly 31 singularities, which was world record at that time. In 1989, Arneau Beauville proved, this is the maximum number of singularities for a quintic. The equation for the shown surface was found by Wolf Barth in 1990.
Read more about world record surfaces here.

Formel
- x^2+y^2–(x^2+y^2+z^2/2)^2 = 0
The Apple (Mathematikon)
We start with an inflatable pool ring, or doughnut, which is called a Torus in mathematics. In order to reconstruct the shape of the apple, the ring was blown up until the insides touch themselves. In this way you create a so-called singularity in the middle, which is formed by two cusps that touch each other.
In general, any point in space can be described by three coordinates - x, y, and z. The given formula creates an apple - that is all points, with their x, y, and z coordinates, which solve the formula. More precisely, it is the surface of the apple without the stem, thus the apple skin.
We can cut the apple open, by only showing the points which are on one side of a cut surface. All points located on the other side are cut off or rather ‘eaten’. Mathematically, this is achieved by using an additional inequality, for example z+4y < 1 would be a slice plane, or x^2+y^2+z^2<R^2 would cut off everything outside a sphere. The bigger the appetite, the smaller the radius of the sphere, which contains the apple core. Knowledge stimulates the appetite!
Logo IMAGINARY France
Using a single formula, you can create images of a cube, a dodecahedron, a rhombic dodecahedron, and an octahedron, just by changing the two parameters a and b.
(ax+by+z)2n+(-ax+by+z)2n+(x+ay+bz)2n+(x-ay+bz)2n+(bx+y+az)2n+(bx+y-az)2n=1
This formula was obtained by constructing a dodecahedron out of three golden rectangles. Their 12 vertices span an icosahedron. The dodecahedron and the icosahedron are dual pairs, meaning faces and vertices are interchanged. Taking the coordinates of the vertices of the icosahedron as coefficients of the simple equation ax+by+cz=d describes a plane orthogonal to the corresponding vertex vector (a,b,c). Since an antipodal pair of vertices yields two parallel planes, we obtain six planes parallel to the twelve faces of a dodecahedron.
Find out more about the formula here.
Watch an animation displaying transformations between these four polyhedra here.
Three Drops
This is a screenshot of an animation created for the movie ‘Imagine a Secret’.
Elliptic curves have deep and beautiful properties. They are plane curves of the type y2 = x3 + a·x + b that have been studied since the XIX century. That equation in the affine plane corresponds to the homogeneous equation y2·z= x3 + a·x·z2 + b·z3, which describes in space a family of algebraic surfaces with two parameters a and b. The computational variation of these equations generates beautiful animations that stimulate our imagination and evoke our mathematical creativity.
Here, three of such algebraic surfaces are seen, each having slightly different parameter values. The droplets actually ‘drop’ at different values of the parameters.
Watch an animation of all three droplets dropping one after another here.
Logo IMAGINARY Taiwan
This is a detail of a pair of solid trefoil knots.
A trefoil knot is basically a closed curve - there are no ends to tie or untie - and it can be obtained by joining the two loose ends of a common overhand knot. You cannot untie it in three dimensions without cutting, which makes it a nontrivial knot. It is actually the simplest nontrivial knot.
The trefoil knot is named after the three-leaf clover (or trefoil). There are two variants: the left-handed and the right-handed trefoil knot, and it is not possible to continuously deform one into the other. This property is called chirality.
In knot theory, the trefoil knot can be classified as a (2,3)-torus knot. It lies on the surface of an unknotted torus in three-dimensional Euclidean space, winding three times around the interior circle line of the torus and two times around its axis of rotational symmetry.
A solid trefoil knot is the boundary surface of a small smooth tubular neighborhood of the trefoil knot curve.
Find out more about how to create solid trefoil knots with the SURFER software here.