실사영평면은 3차원 공간(R3)에서 원점을 지나는 직선들로 이루어진 공간입니다. 수학자 야곱 슈타이너(Jacop Steiner)가 로마에 머물 때, 실사영평면에서 R3로의 사상을 생각해냈습니다. 만들어진 곡면은 자기 자신과 만납니다. 이를 Roman 곡면 혹은 Steiner 곡면이라고 부릅니다.

원점은 삼중점이 되고 각 좌표 평면은 곡면과 접합니다. 원점 외에, 각 좌표축 위의 선분은 모두 이중점들로 이루어졌고, 그 6개 선분들 끝에 각각 pinch point가 있습니다.

사진을 보면, 6개의 Roman 곡면 조각들이 노란색 Roman 곡면을 둘러싸고 각 6개의 pinch point에서 만나고 있습니다. 곡면의 고차원의 대칭 구조가 돋보입니다.

왼쪽의 사진은 영상 ‘Imagine a Secret‘을 위해 만들어진 애니메이션의 스크린샷입니다.

타원곡선은 깊고 아름다운 성질을 가지고 있는데, y2 = x3 + a·x + b 꼴의 평면곡선으로서 19세기부터 연구되었습니다. 아핀 평면 위의 이 방정식은 y2·z= x3 + a·x·z2 + b·z3 꼴의 동차방정식에 대응되는데, 공간에서는 a와 b를 매개변수로 가지는 대수곡면들의 집합으로 표현됩니다. 이 방정식의 변화는 아름다운 애니메이션을 만들어 내 수학적 창의력과 상상력을 자극합니다.

사진에는 세가지 대수곡면(빨강, 초록, 노랑)이 있어, 각각 사뭇 다른 변수값을 갖고 있습니다. 또 이미지 중앙에 반투명한 검정 구체가 있어 살짝 수수께끼를 남깁니다. 색칠된 곡면 세 개 중 밝고 곡선 같은 부분들은 검정 구체에 포함되지 않습니다. 하지만 구체의 일부분은 그래도 SURFER 프로그램으로 만들어진 보이는 공간을 포함하고 있습니다. 

곡면을 보여주는 애니메이션을 보시려면 여기를 클릭하십시오.

뫼비우스의 띠의 경계는 닫힌 곡선 한 개에 불과한데, 이를 원판의 경계에 꿰맨다고 생각해보십시오! 생성되는 닫힌 곡면에는 뫼비우스의 띠가 그대로 포함되어있기 때문에 방향을 줄 수 없습니다(바깥과 안쪽을 구분하지 못하고 모두 같다고 봅니다). 따라서 이렇게 만든 도형은 3차원 공간에선 자기교차가 있어야 합니다. 하지만 자기교차가 뾰족하고 날카로운 모서리 없이 매끄럽게 가능할까요?

저명한 수학자 다비드 힐베르트(David Hilbert)는 제자 베르네르 보이(Werner Boy)에게 그게 불가능함을 보이라고 과제를 내주었습니다. 하지만 놀랍게도 1901년, Boy는 조건을 만족하는 매끄러운 곡면을 만들어냈습니다. 보이는 서로 평행한 평면들의 집합과 곡면의 교차선에 대응하는 곡선들을 제시하여 만들어냈습니다. 

이 사진을 보면, Boy곡면의 조각을 두 개 볼 수 있습니다(서로 거울대칭인). 평면으로 절단되지 않고 같은 중심에 각기 다른 반지름을 가진 구체 두 개로 절단된 조각들입니다.

보이 곡면의 시각화를 위해 쓰인 방정식은 프랑수와 아페리(Francois Apery)가 발견하였습니다.

세 번 꼬인 뫼비우스 띠 한 쌍입니다.

뫼비우스의 띠는 꽤 잘 알려진 고전적인 개념인데, 기하학과 위상수학에서 전문 수학자 뿐만 아니라 많은 사람들의 관심을 끌고 있습니다. 이 모양은 종이 띠를 꼬아 붙여서 만들 수 있습니다. 양끝을 k번 꼬아 붙여주면(k는 홀수) k번 뒤틀린 뫼비우스의 띠가 만들어집니다. k가 짝수면, 뒤틀린 원기둥이 나옵니다. 

뫼비우스의 띠 근처의 튜브 형 근방(tubular neighborhood)의 형태의 경계를 입체(solid) 뫼비우스의 띠라고 합니다. 

SURFER 소프트웨어로 입체 뫼비우스의 띠를 만드는 것에 대해 더 알고 싶으시면 여기를 클릭하십시오.

방정식 x² y² + y² z² + x² z² + xyz = 0 이 나타내는 모양은 야곱 슈타이너(Jakob Steiner)에 의해 발견되었습니다. 1844년 로마에 머무를 때 그 기하학적 성질들을 연구했다고 하여 로만(Roman) 곡면이라고 불립니다. 하지만, 1863년 그가 죽고, 이 곡면과 Steiner의 결과를 논문에 처음 실은 것은 그의 친구 카를 바이어스트라스(Karl Weierstrß)였습니다.

사진에는 원점을 중심으로 대칭을 이루고 있는 18개의 Roman 곡면들을 볼 수 있습니다. 각 곡면은 서로 교차하도록 원점에서 각각 1개 또는 2개의 좌표축을 따라 살짝 평행이동하였습니다. 덧붙여, 이 사진에는 전체 구조의 작은 부분만 나타나 있습니다: 원점을 중심으로 작은 구형 근방 내에 있는 모든 부분. 근방 밖의 부분은 모두 누락되어있습니다.

Roman 곡면은 방향을 가지지 않습니다-안과 바깥이 구분되지 않고 딱 한 쪽만 존재합니다. 그래도 SURFER 프로그램은 색을 두 개 부여합니다. 여기 보시면 각 곡면은 첫번째 색은 밝은 색인 반면, 두번째 색은 검정색입니다. 배경색 또한 검정색입니다.

2014년 대한민국 서울에서 열린 ICM의 NIMS-IMAGINARY 전시회 로고는 ICM 로고와 유사하게 수학적 질서를 따르는 성장을 대변하고 늦게 시작한 이들의 꿈과 희망을 상징합니다. 이 S자 로고는 서울의 S와 태극기의 ‘태극’ 의미를 나타냅니다. 태극은 음과 양의 조화를 상징합니다. 양을 나타내는 빨간색은 사랑과 열정을 뜻하고, 음을 나타내는 파란색은 지성과 꿈을 뜻합니다. 한편, 양과 음 둘다 같은 색과 모양에서 시작함으로써 우주의 하나됨을 나타내고 있습니다. 

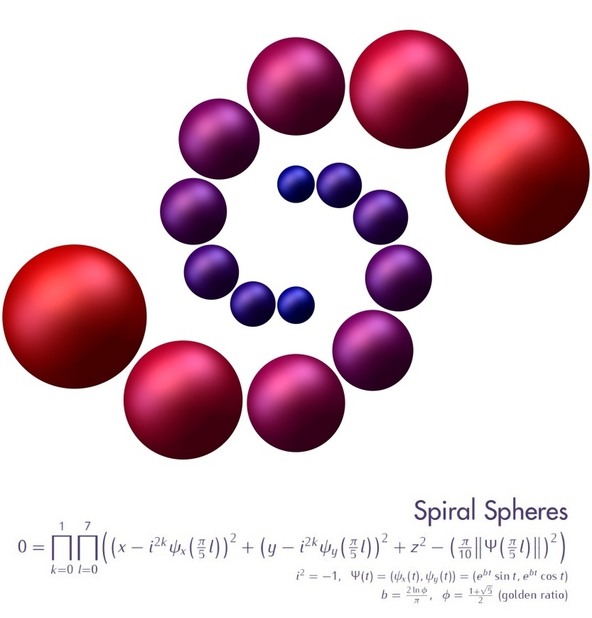
NIMS-IMAGINARY 전시회의 나선형 구체 로고는 두 황금 나선 위에 중심이 있는 구체 16개를 보여주고 있습니다(나선은 각각 k=0, k=1). 프사이 함수는 나선 곡선의 매개변수함수입니다. 각 구체의 반지름은 원점에서부터의 거리에 비례하는데, 곧 프사이 벡터의 크기와 같습니다.

나선형 구체에 관한 애니메이션을 보고 싶으시면 여기를 클릭하십시오.

‘유럽에서의 수학’(Mathematics in Europe, MaTiE) 프로젝트를 위한 로고는 토글리아티(Togliatti)의 5차식의 두 가지 버전을 결합하여 만들어졌습니다. Togliatti 5차식은 SURFER 소프트웨어에 통합된 갤러리에 있습니다. 유럽풍의 색이 어우러졌고 오각형 별 모양을 취하고 있습니다. 이는 국가간의 연계와 상호관계, 그리고 함께 일할 때의 강한 모습을 상징합니다. 

1937년, 유지니오 규세프 토글리아티(Eugenio Giuseppe Togliatti)는 정확히 31개의 특이점을 가지는 5차원 곡면이 존재한다는 것을 증명해 당시 세계 기록을 세웠습니다. 1989년, 아르누 뷰빌(Arneau Beauville)은 이 값이 5차원 특이점의 최대치라는 것을 증명했습니다. 해당 곡면에 대한 방정식은 1990년 울프 바스(Wolf Barth)에 의해 발견되었습니다. 

세계기록 곡면에 대해 더 알고 싶으시다면 여기를 클릭하십시오.

공식 하나만 가지고도 매개변수 a, b값에 따라 육면체, 십이면체, 마름모 십이면체(rhombidodecahedron), 팔면체를 만들어낼 수 있습니다. 

(ax+by+z)2n+(-ax+by+z)2n+(x+ay+bz)2n+(x-ay+bz)2n+(bx+y+az)2n+(bx+y-az)2n=1

이 공식은 세 개의 황금사각형에서 십이면체를 만들면서 나왔습니다. 여기에 생기는 12개의 꼭지점은 이십면체를 만듭니다. 이 십이면체와 이십면체를 쌍대(dual pair)이라고 하는데, 서로의 면과 꼭지점이 바뀌었다는 뜻입니다. 이십면체의 꼭지점 좌표를 계수로 가지는 방정식 ax+by+cz=d는 해당하는 점벡터 (a, b, c)에 수직한 평면을 나타냅니다. 서로 원점대칭인 두 점벡터는 각각 평행한 평면을 나타내니, 십이면체의 12면에 평행한 6개의 평면을 얻을 수 있습니다.

공식에 대해 더 알고 싶으시다면 여기를 클릭하십시오.

네 가지 다면체간의 변환을 보여주는 애니메이션을 보고 싶으시다면 여기를 클릭하십시오.

왼쪽의 사진은 영상 ‘Imagine a Secret‘을 위해 만들어진 애니메이션의 스크린샷입니다.

타원곡선은 깊고 아름다운 성질을 가지고 있는데, y2 = x3 + a·x + b 꼴의 평면곡선으로서 19세기부터 연구되었습니다. 아핀 평면 위의 이 방정식은 y2·z= x3 + a·x·z2 + b·z3 꼴의 동차방정식에 대응되는데, 공간에서는 a와 b를 매개변수로 가지는 대수곡면들의 집합으로 표현됩니다. 이 방정식들의 변화는 아름다운 애니메이션을 만들어내 수학적 창의력과 상상력을 자극합니다.

여기 그러한 대수곡면이 세 개 보입니다. 각각의 곡면은 사뭇 다른 변수값을 가지고 있습니다. 작은 방울들은 실제로 서로 다른 변수값에서 ‘떨어집니다.’

세 방울이 순차적으로 떨어지는 애니메이션을 보고 싶으시다면 여기를 클릭하십시오. 

이 사진은 속이 꽉 찬 trefoil 매듭 한 쌍에 대한 자세한 모습입니다.

Trefoil 매듭은 기본적으로 닫힌 곡선- 묶거나 풀 수 있는 끝이 없는 곡선 - 입니다. 그리고 공통의 common overhand 매듭의 느슨한 양 끝을 연결하여 만들 수 있습니다. 3차원에서는 자르지 않고서는 매듭을 풀 수가 없어 자명하지 않은 매듭이라고 합니다. 

Trefoil 매듭은 세잎클로버(혹은 삼엽)를 따서 이름이 지어졌습니다. 이 매듭은 왼손잡이와 오른손잡이, 두 종류의 모양이 있는데, 두 모양은 연속적으로 상호 변환이 불가합니다. 이 성질을 카이랄성(chirality)라고 합니다.

매듭이론에서 trefoil 매듭은 (2,3)-토러스 매듭으로 분류될 수 있습니다. 3차원 유클리드 공간의 꼬이지 않은 토러스 표면에 놓여있어, 토러스 경선 방향으로 세 번 감고 회전대칭축을 두 번 감습니다. 

고체(solid) trefoil 매듭은 trefoil 매듭 곡선의 매끄러운 작은 관 모양 근방의 경계곡면이라고 볼 수 있습니다. 

SURFER 소프트웨어로 고체 trefoil 매듭을 만드는 법을 알고 싶으시다면 여기를 클릭하십시오.