The Mandelbox, an artistic and geometric journey
The Mandelbox is a mathematical object that was first presented by Tom Lowe (aka Tglad) early in 2010. It can represent properties of the Mandelbrot set in dimensions other than the two of the Mandelbrot set. In contrast to Quaternion Fractals or the Mandlbulb, which follow a formal mathematical path with the Mandelbrot iteration z=z²+c, the Mandelbox follows a purely geometrical approach. On the one hand, this allows representations in any number of dimensions. On the other hand, the shape is relatively independent from the shapes known from Mandelbrot and Julia sets.
Since up to now only graphical applications are known, higher-dimensional variants hardly play a role. The vast majority of the images of the Mandelbox are three dimensional variants. (There are some three-dimensional representations of a 4d Mandelbox or two-dimensional displays, but only a few)
Formel
- v = s·ballFold(r, f·boxFold(v)) + c
Mandelbox default
The approach
Fundamental transformation of the Mandelbrottian iteration (z=z²+c) is the squaring of a complex number represented in z². In the vectorial view this corresponds to a rotational extension of the position vector of a point. In other words, this is a circular transformation with subsequent scaling. In the Mandelbox, a spherical transformation is performed (the so-called BallFold) with subsequent scaling. This is already the whole trick. There is further a BoxFold for the shape and – as with Mandelbrot – the addition of a constant c.
Please consider that this reflects a most simplified and pointed geometric view. The algebraic view is more complex and needs a high level of abstraction, but gives us the opportunity to calculate and study this object. In the end formulas (see bottom left) and algorithms, does not tell us much about the shape created with a certain parameter set and unforunately humans have no real sense for that kind of math. So we need to try out. And here the geometric view is pretty useful.
In most common 3d fractal software – Mandelbulber and Mandelbulb3d – the default starting Parameter at a scale of two
Tglad's trick
A purely bold display of the relationship between the Mandelbox and the Mandelbrot set. A formal mathematical connection cannot be derived from this.
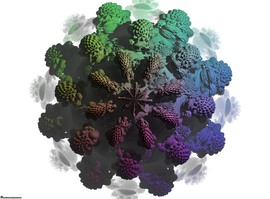
the harvest
An image of 2011, from the early days of the Mandelbox. The Mandelbox can also be scaled negatively, which corresponds to a rotation of 180°. With additional rotations of about 0°±15°, images like this one are created. One of the first parameters, I converted to Mandelbulb3d. With help of Jens Dierks (aka Jesse) - the Programmer of M3d.
In fact Jesse wrote a little tool, that converts rotation angles between the programmes. Rotations are not commutative in three dimensions (means x+y+z ≠ z+y+x) and m3d rotates x-axis first and Mandelbulber the z-axis.
This tool can still be found at the old fractal forums
Image published in: Benoit Mandelbrot: A life in many dimensions
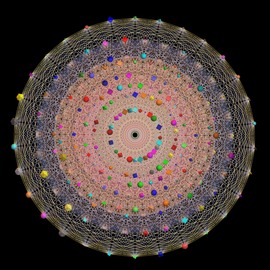
sea invader
Another image with a negative scale and rotated folding planes. The picture was part of the exhibition Imaginary in Nuremberg (Form und Formel mathematischer Fantasie)
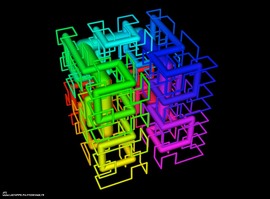
vintage circuit
An unrotated Mandelbox at a scale of -2,5. Shape was developed in Mandelbulber, ported to Mandelbulb3d and rendered in M3d MC renderer. Part of Maniac Art, Galerie Schauraum Worms
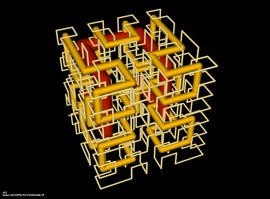
zero g
the derivations
Meanwhile, there are countless modifications of the Mandelbox, which reproduce the concept in a different form with different additional parameters or other folding methods.Here I will only present one of the ‒ geometrically as well as artistically ‒ most interesting approaches.
Amazing Surface is based on a proposal by Pablo Andreoli (aka Kali) and is ‒ to put it simply ‒ a somewhat extended 2d Madelbox. All folds are limited to two axes, only the folding planes can be rotated 3-dimensionally. Unfortunately, at this point we leave the realm of exact mathematics. The implementations in different software do not lead to directly comparable results - partly due to the principle (e. g. programmes execute non-commutative rotations in different order).
