Richard Palais und Luc Benard
MathematikerInnen haben seit dem antiken „Upgrade“ von in Sand gezeichneten Diagrammen zu eingeritzten Tontafeln immer die Fortschritte der Grafik-Kunst verwendet, um die Art und Weise zu verbessern, wie sie mathematische Konzepte im Unterricht und in der Forschung präsentierten. Daher ist es keine Überraschung, dass das Paradigma der neuen modernen Computertechnologie spektakuläre neue Möglichkeiten bietet, um immer komplexere mathematische Objekte und Prozesse zu visualisieren. 3D-XplorMath ist ein mathematisches Visualisierungsprogramm, um die neuen Technologien voll auszuschöpfen. Es ist eigentlich ein virtuelles Mathematik- Museum mit einer intuitiven Benutzeroberfläche, die es auch Nicht-MathematikerInnen erlaubt, die Vorzüge der neuen graphischen Möglichkeiten und die visuelle Schönheit zu erleben, die vielen Gebieten der Mathematik eigen ist.
Es war eine willkommene Überraschung für die EntwicklerInnen des Programms, dass einige KünstlerInnen so von den ästhetischen Möglichkeiten, die sie in den vielen von 3D-XplorMath erzeugten Bildern entdeckten, angezogen wurden, dass sie diese als Thema für ein neues Genre einer künstlerischen Bildwelt nahmen. Luc Benard ist ein außerordentliches Mitglied dieser neuen Gruppe von mathematisch orientierten Künstlern. Während Luc darin spezialisiert ist, die Schönheiten von Fraktalen und Flächen hervorzuheben, ist er der Meinung, dass jedes mathematische Gebiet seine eigene Schönheit besitzt, die in der Eleganz seiner Konzepte, Theorien, Formeln und wunderbaren Bildern zu finden ist. Einige seiner Kreationen sind in dieser Ausstellung zu sehen, und Richard Palais hat ihn auch als Mitglied des 3DXM Konsortiums rekrutiert, um eine Galerie der Mathematik- Kunst für das virtuelle Museum zu schaffen.
Links
http://3D-XplorMath.org
http://virtualmathmuseum.org
http://virtualmathmuseum.org/mathart/MathematicalArt.html
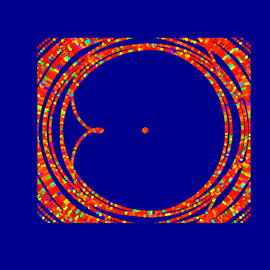
Lyapunov play
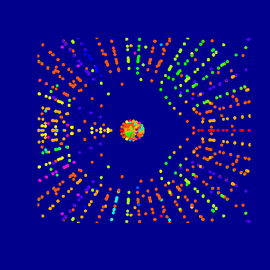
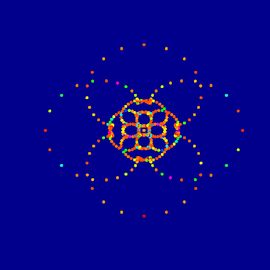
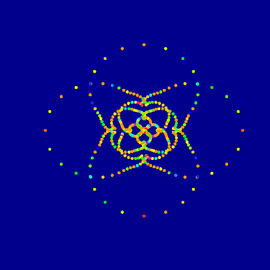
Mario Markus des Max-Planck-Instituts für molekulare Physiologie hat dynamische Systeme verwendet, um die Evolution von Tierbeständen - den zeitlichen Wandel von Nahrung, Fruchtbarkeit, Größe usw. - zu studieren, wobei die Dynamik fordert, dass das Fortpflanzungsvermögen quasi-periodisch zwischen zwei Werten pendelt. Solche Systeme können sowohl einen stabilen Zyklus als auch chaotische Evolution darstellen, abhängig vom Fortpflanzungsvermögen. Die Stabilität oder das Chaos können durch Berechnung des sogenannten Lyapunov Exponenten analysiert werden. (Lyapunov war ein russischer Mathematiker Ende des 19. Jahrhunderts).
Markus-Lyapunov Bilder sind Farbverknüpfungen des Lyapunov Exponenten gegen die Fruchtbarkeit, entlang je horizontaler und vertikaler Achsen. Nur der Stabilitätsbereich wird dargestellt. Chaos (entsprechend einem positiven Lyapunov Exponenten) ist dunkelblau gekennzeichnet. Während der Exponent von 0 zu minus unendlich wandert, wandelt sich der Farbton von hell zu dunkel. Bei Null, der Chaos-Schwelle, springt die Farbe plötzlich von dunkelblau zu hell. Bei den Farbkombinationen wurde Vieles beliebig gewählt, was Spielraum für ästhetische Überlegungen gibt. Das Bild besteht aus sieben originalen Markus-Lyapunov Bildern, die nachbearbeitet und überlagert wurden.
Studie von Gleichungen
Diese fraktalen Bilder entstehen durch Einsetzen verschiedener Gleichungen in das Windows Programm Flarium24 von Stephen Ferguson, mit 40 Iterationen und dem Filter
rr+=atan(fabs(dzy/dzx))*atan(fabs(dzx/dzy))*2.
Sie wurden im Photoshop zusammengestellt, und imitieren durch die Schrift und Färbung die Zeichnungen von Leonardo DaVinci. Obwohl diese Bilder mathematischen Ursprung haben, empfinden sie viele Menschen als ästhetisch, unabhängig von ihrer Herkunft.
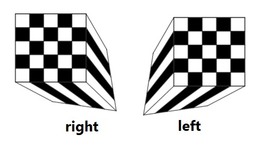
Eine dreifach periodische Niveau-Fläche
Die grün gefärbte Fläche besitzt drei orthogonale Translations- Symmetrien. Sie ist durch die folgende trigonometrische Gleichung gegeben:
4*(cos x*cos y+cos y*cos z+cos z*cos x) - 3*cos x *cos y *cos z = -2.4
Eine einzelne Zelle kann als Kammer betrachtet werden mit Schläuchen zu den Ecken und Kanten des Würfels. Diese Fläche approximiert die minimale P-Fläche, die 1880 von Karl Hermann Amandus Schwartz (eh. Professor in Halle, Göttingen und Berlin) gefunden wurde. Vor kurzem wurde diese Fläche von Materialwissenschaftlern untersucht, die sie und ähnliche Flächen verwenden, um sogenannte Block-Copolymere zu modellieren. Das Original-Modell stammt von David A. Hoffman. Es wurde texturiert und in eine Szene gesetzt, die ästhetisch dazupasst. Erzeugt mit dem Programm Bryce.
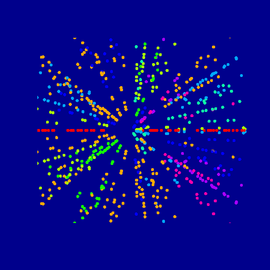
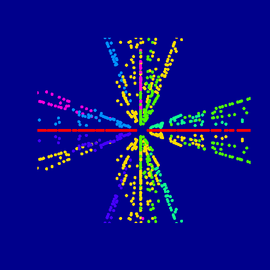
Wada Bereiche
Dieses Bild spiegelt Resultate von Experimenten mit chaotischer Streuung wider. Die Ausgangssituation sind 4 identische, hoch reflektierende Kugeln, die in Pyramidenform angereiht sind, sodass jede Kugel jede andere berührt. Wenn Sie in die Zwischenräume der drei Kugeln blicken, sehen Sie ein dreidimensionales Fraktal mit der sogenannten Wada Eigenschaft. Diese ist nach einem japanischen Mathematiker benannt, der solche räumlichen Teilungen im Jahr 1917 untersuchte. Die Wada Eigenschaft bezeichnet ein diskretes dynamisches System mit drei Anziehungsbecken, die so verbunden sind, dass jeder Punkt des Randes eines Beckens auch der Rand aller anderen ist. Das Bild wurde mit dem Programm Bryce erzeugt.
Stillleben: fünf Glasflächen auf einer Tischplatte
Dieses Bild entstand in der Zusammenarbeit des Mathematikers Richard Palais und des Grafik-Künstlers Luc Benard. Es wurde mit dem ersten Preis des 2006 Visualization Challenge der Zeitschrift Science in der Kategorie „Illustration“ ausgezeichnet und war am 22.9.2006 auch auf dessen Cover zu sehen. Die fünf mathematischen Flächen sind, angefangen unten links, im Uhrzeigersinn: die Kleinsche Flasche, das symmetrische 4-Noid, die Breather Fläche, die Boysche Fläche und die Sievert-Enneper Fläche. Die Flächen in diesem Bild wurden von Palais mit dem Programm 3D_XplorMath entworfen und dann von Benard im Programm Bryce erzeugt.