4D en 3D

La 120-celda es un politopo regular en dimensión cuatro. La 120-celda está formada por 120 dodecaedros iguales adosados por sus caras (720 pentágonos). Tiene 600 vértices y 1200 lados. Este politopo es, en dimensión cuatro, el análogo al dodecaedro en dimensión tres, que tiene 12 pentágonos regulares iguales adosados por sus lados. Tiene 20 vértices y 30 lados. El dodecaedro lo podemos ver proyectado en la esfera S2 (recordar un balón de futbol), o mediante proyección estereográfica en un plano, como en la figura.

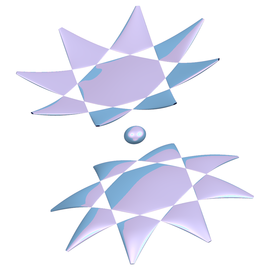
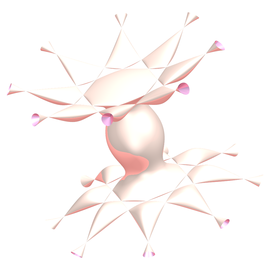
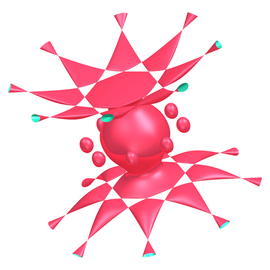
Las imágenes de este panel y del siguiente muestran distintos puntos de vista de la representación de la 120-celda (contenida en la esfera S3) en el espacio tridimensional usual. Esta imagen es la de su proyección estereográfica. Se observa que los dodecaedros están curvados de manera que los pentágonos son trozos de esferas y las aristas trozos de circunferencias.

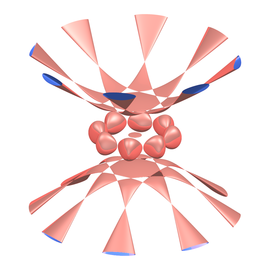
Futbol en 4D

En la imagen, la 120 celda se ha proyectado primero desde su centro sobre la esfera S3 que la circunscribe (que bien podría ser, por analogía con la figura del texto anterior, el balón de futbol de los habitantes de la cuarta dimensión), y después se ha tomado su ‘sombra’ en el espacio 3D iluminándolo desde un punto situado a una cierta distancia, en dirección perpendicular, del centro de una de sus ‘caras’. La ‘cara’ más cercana al punto de iluminación queda visualizada como el dodecaedro exterior. La ‘cara’ opuesta corresponde al dodecaedro más pequeño en el centro de la imagen. Como en la imagen anterior, los dodecaedros están curvados de manera que los pentágonos son trozos de esferas y las aristas trozos de circunferencias. La ilustración muestra como sería la ‘sombra’ de la 120 celda iluminándola directamente (sin proyectar primero sobre la esfera) desde un punto situado perpendicularmente sobre el centro de una de sus ‘caras’.

El arte de la cartografía

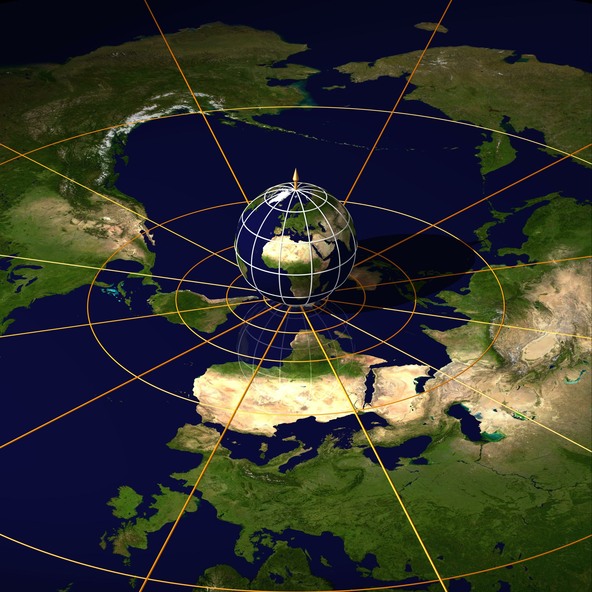
Durante siglos, cartógrafos y matemáticos han estado buscando la manera de proyectar la superficie terrestre sobre un plano para obtener mapas correctos. Es decir, mapas sobre los que poder medir correctamente la longitud de un río, la distancia entre dos ciudades, el alcance de un misil, la superficie de un bosque o el rumbo de viaje en navegación marítima o aérea.

Por desgracia, esto no es posible: la curvatura de Gauss K de la esfera es una constante positiva, la del plano es nula y sin embargo K debe preservarse por transformaciones “isométricas” (las que generan mapas correctos). Así, si se intenta aplanar la mitad de una pelota de goma, esta se deformará y rasgará, modificándose las distancias, la geometría interna de la esfera. En conclusión, todos los mapas son falaces en algún sentido.

La transformación mostrada en la imagen (una entre cientos de las existentes) es la proyección estereográfica que proyecta los puntos de la superficie terrestre desde el Polo Norte sobre un plano tangente al Polo Sur. Esta preserva los rumbos y transforma los meridianos en rectas que pasan por el Polo Sur y los paralelos en circunferencias concéntricas.

Matemática no hay más que una

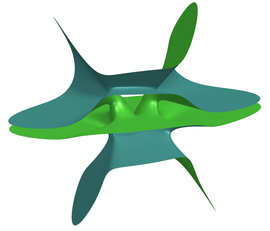
Otra bella imagen de un flujo modular relacionado con el nudo Trébol. Para una introducción a los sistemas dinámicos modulares, y su relación con la teoría de las curvas elípticas y la teoría de números, se puede consultar el magnífico artículo [+]. Su subtítulo, “A tangled tale linking lattices, knots, templates, and strange attractors …”, apunta al hecho, como una más entre innumerables muestras, de que en la ‘realidad matemática’ todo está íntimamente interconectado, y que en buena medida el oficio matemático, por no llamarle arte, tiene por objeto poner de manifiesto nuevas conexiones, nuevos caminos que unen inesperadamente los conceptos. [+] Étienne Ghys, Jos Leys: Lorenz and Modular Flows: A Visual Introduction. Monthly Essays on Mathematical Topics, American Mathematical Society, 2006.

[+] Étienne Ghys, Jos Leys: Lorenz and Modular Flows: A Visual
Introduction.
Monthly Essays on Mathematical Topics, American Mathematical
Society, 2006

¿Puede la Aritmética prescindir de los Sistemas dinámicos?

La Aritmética estudia los números, la Geometría y la Topología estudian las formas, la Dinámica estudia el movimiento, el cambio de las configuraciones al transcurrir el tiempo. Una descripción de este estilo podría hacer pensar que las fronteras entre estos dominios están bien definidas y que entre ellos hay poca interacción. Sin embargo se constata todo lo contrario, esto es, que entre los distintos dominios de las matemáticas hay profundas interconexiones. La imagen ilustra un caso elocuente. Esta embarullada topología es una visualización de un flujo de Anosov. Más concretamente, es el flujo de uno de los sistemas dinámicos ‘modulares’, los cuales resultan ser fundamentales para el estudio de los números enteros, y en particular de los números primos.