The Heidelberg Laureate Forum Foundation invites you to visit the exhibition “Mathematics of Planet Earth” at Karlstorbahnhof in Heidelberg, Germany! It runs from July 5 to Aug 2, 2015, for the first time in Heidelberg. It offers a big variety of exciting adventures for children and adults alike.
Jos Leys, Étienne Ghys and Aurélien Alvarez
The following pictures are images from two chapters of the film “Dimensions, a walk through mathematics” rendered in high-resolution. In one chapter, Hipparchus shows us how to describe the position of any point on Earth with two numbers and explains the stereographic projection. In another chapter, mathematician Ludwig Schläfli talks about objects that live in the fourth dimension, and shows a parade of four-dimensional polytopes, strange objects with 24, 120 and even 600 faces! Two pictures of the exhibition that look like knots are special.
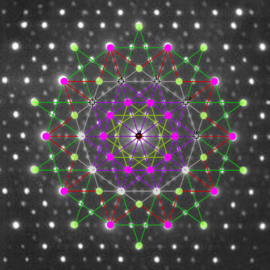
The Hecatonicosachoron
Also called the “120-cell”, this is a regular polytope in four dimensions. It is the four dimensional analogue of the three dimensional dodecahedron, that has 12 pentagonal faces, 20 vertices and 30 edges.
The hecatonicosachoron has 120 ‘faces’, but they are in 4 di- mensions, so they are in reality three-dimensional faces: they are all dodecahedrons! The two-dimensional faces of these dodeca- hedrons are of course pentagons, and there are 720 of them. There are 600 vertices and 1200 edges.
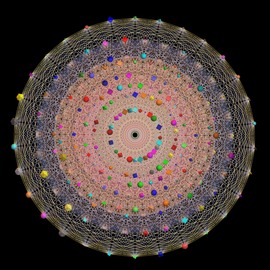
The Hecatonicosachoron (Inside)
The images in the exposition show the 120-cell drawn through stereographic projection, but of course not the normal stereo- graphic projection from a sphere in our three dimensional space on to a plane through the south pole. This is a stereographic projection from a sphere in four dimensions onto our space of three dimensions.
This projection shows the symmetries of the 120 cell very well. Note also that the two dimensional faces of the object are all pieces of spheres, and that the vertices are all segments of cir- cles.
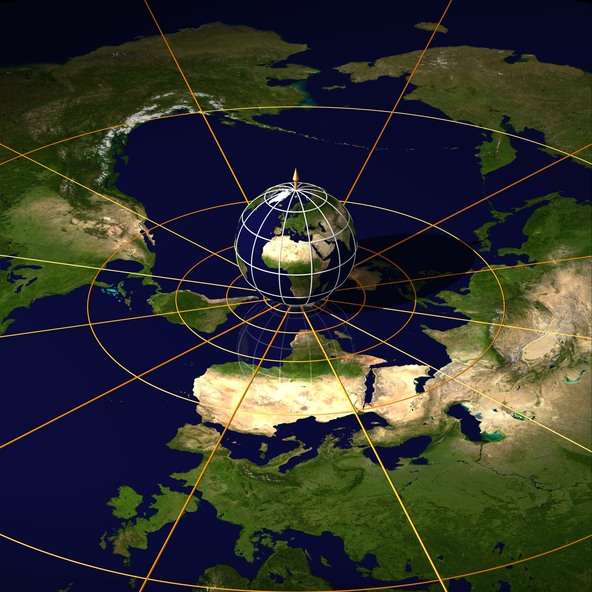
Stereographic Projection
Points on a sphere are projected from the north pole onto a plane that is perpendicular to the axis through the poles, usually the plane through the south pole.
All points of the sphere can thus be projected onto the plane, except for the north pole itself, and a point at infinity is therefore associated with the north pole.
Stereographic projection will project circles on the sphere onto circles in the plane, and preserves angles.
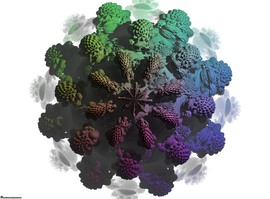
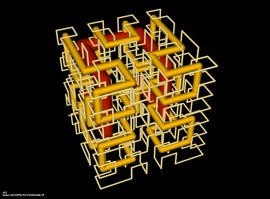
Real Matrix
Explaining these images in a few lines is very difficult. More information can be found in this article.
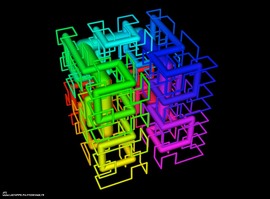
Anosov Flow
Explaining these images in a few lines is very difficult. More information can be found in this article.