Stephan Klaus: Knots
Galerie
Stephan Klaus: Knots
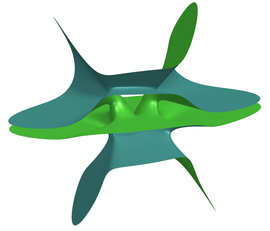
Stephan Klaus is professor of topology and works at the Mathematisches Forschungsinstitut Oberwolfach. He used SURFER to visualize knotted surfaces. He found a method to construct such polynomials by Fourier decomposition and algebraic variable elimination for every knot type.

Formel
- ((a-b)\cdot (x\cdot (x^2+y^2-z^2+1)-2\,yz)-(2a+2b+ab)\cdot (x^2+y^2))^2 -{(x^2+y^2)\cdot ((a+b)\cdot (x^2+y^2+z^2+1)+2\cdot (a-b)\cdot (yz-x))}^2=0
Möbiusband 1
Lizenz CC BY-NC-SA-3.0

Formel
- ((a-b)\cdot (x\cdot (x^2+y^2-z^2+1)-2\,yz)-(2a+2b+ab)\cdot (x^2+y^2))^2 -{(x^2+y^2)\cdot ((a+b)\cdot (x^2+y^2+z^2+1)+2\cdot (a-b)\cdot (yz-x))^2}=0
Möbiusband 1
Lizenz CC BY-NC-SA-3.0

Formel
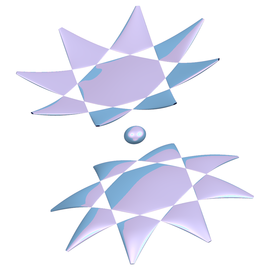
- ((b^2x^2+a^2y^2)\cdot (x^2+y^2)+b^2\cdot (-x+yz)^2+a^2\cdot(y+xz)^2-a^2b^2\cdot (x^2+y^2))^2 -{4\cdot (x^2+y^2)}\cdot (b^2x\cdot(-x+yz)-a^2y\cdot (y+xz))^2=0
Doppeltes Möbiusband
Lizenz CC BY-NC-SA-3.0

dreifaches Möbiusband 1
Lizenz CC BY-NC-SA-3.0

dreifaches Möbiusband 2
Lizenz CC BY-NC-SA-3.0

Formel
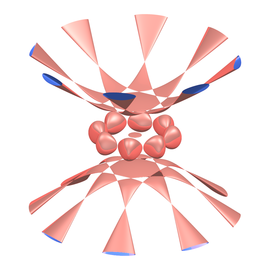
- (-8\cdot (x^2+y^2)^2\cdot (x^2+y^2+1+z^2+a^2-b^2) +{4a^2\cdot (x^3-3\,xy^2)\cdot z^2} +{4a^2\cdot (2\cdot (x^2+y^2)^2-(x^3-3\,xy^2)\cdot (x^2+y^2+1))} +{8a^2\cdot (3\,x^2y-y^3)\cdot z})^2 -{(x^2+y^2)\cdot ({2\cdot (x^2+y^2)\cdot (x^2+y^2+1+z^2+a^2-b^2)^2} +{8\cdot (x^2+y^2)^2} +{4a^2\cdot (2\cdot (x^3-3\,xy^2)-(x^2+y^2)\cdot (x^2+y^2+1))} -{8a^2\cdot (3\,x^2y-y^3)\cdot z} -{4\cdot(x^2+y^2)\cdot a^2z^2})^2}=0
Kleeblattknoten 1
Lizenz CC BY-NC-SA-3.0

Formel
- (-8\cdot (x^2+y^2)^2\cdot (x^2+y^2+1+z^2+a^2-b^2) +{4a^2\cdot (2\cdot(x^2+y^2)^2-(x^3-3\,xy^2)\cdot (x^2+y^2+1))} +{8a^2\cdot (3\,x^2y-y^3)\cdot z} +{4a^2\cdot (x^3-3\,xy^2)\cdot z^2})^2 -{(x^2+y^2)\cdot (2\cdot (x^2+y^2)\cdot (x^2+y^2+1+z^2+a^2-b^2)^2 +{8\cdot (x^2+y^2)^2} +{4a^2\cdot (2\cdot (x^3-3\,xy^2)-(x^2+y^2)\cdot (x^2+y^2+1))} -{8a^2\cdot (3\,x^2y-y^3)\cdot z} -{4\cdot (x^2+y^2)\cdot a^2z^2})^2}=0
Kleeblattknoten 2

Formel
- (-8\cdot (x^2+y^2)^2\cdot (x^2+y^2+1+z^2+a^2-b^2)+4a^2\cdot (2\cdot (x^2+y^2)^2-(x^3-3\,xy^2)\cdot (x^2+y^2+1))+8a^2\cdot (3\,x^2y-y^3)\cdot z+4a^2\cdot (x^3-3\,xy^2)\cdot z^2)^2-(x^2+y^2)\cdot (2\cdot(x^2+y^2)\cdot (x^2+y^2+1+z^2+a^2-b^2)^2+8\cdot (x^2+y^2)^2+4a^2\cdot (2\cdot (x^3-3\,xy^2)-(x^2+y^2)\cdot (x^2+y^2+1))-8a^2\cdot (3\,x^2y-y^3)\cdot z-4\cdot (x^2+y^2)\cdot a^2z^2)^2
Kleeblattknoten 3
Lizenz CC BY-NC-SA-3.0

Formel
- (-8\cdot (x^2+y^2)^2\cdot (x^2+y^2+1+z^2+a^2-b^2)+4a^2\cdot (2\cdot (x^2+y^2)^2-(x^3-3\,xy^2)\cdot (x^2+y^2+1))+8a^2\cdot (3\,x^2y-y^3)\cdot z+4a^2\cdot (x^3-3\,xy^2)\cdot z^2)^2-(x^2+y^2)\cdot (2\cdot (x^2+y^2)\cdot (x^2+y^2+1+z^2+a^2-b^2)^2+8\cdot (x^2+y^2)^2+4a^2\cdot (2\cdot (x^3-3\,xy^2)-(x^2+y^2)\cdot (x^2+y^2+1))-8a^2\cdot (3\,x^2y-y^3)\cdot z-4\cdot (x^2+y^2)\cdot a^2z^2)^2=0
Kleeblattknoten 4
Lizenz CC BY-NC-SA-3.0

Formel
- (-8\cdot (x^2+y^2)^2\cdot (x^2+y^2+1+z^2+a^2-b^2)+4a^2\cdot (2\cdot (x^2+y^2)^2-(x^3-3\,xy^2)\cdot (x^2+y^2+1))+8a^2\cdot (3\,x^2y-y^3)\cdot z+4a^2\cdot (x^3-3\,xy^2)\cdot z^2)^2-(x^2+y^2)\cdot (2\cdot (x^2+y^2)\cdot (x^2+y^2+1+z^2+a^2-b^2)^2+8\cdot (x^2+y^2)^2+4a^2\cdot (2\cdot (x^3-3\,xy^2)-(x^2+y^2)\cdot (x^2+y^2+1))-8a^2\cdot (3\,x^2y-y^3)\cdot z-4\cdot (x^2+y^2)\cdot a^2z^2)^2=0
Kleeblattknoten 5
Lizenz CC BY-NC-SA-3.0

Formel
- (-8\cdot (x^2+y^2)^2\cdot (x^2+y^2+1+z^2+a^2-b^2)+ {4a^2\cdot(2\cdot (x^2+y^2)^2 -(x^3-3\,xy^2)\cdot (x^2+y^2+1))} +{8a^2\cdot(3\,x^2y-y^3)\cdot z} +{4a^2\cdot (x^3-3\,xy^2)\cdot z^2})^2 -(x^2+y^2)\cdot ({2\cdot (x^2+y^2)}\cdot (x^2+y^2+1+z^2+a^2-b^2)^2 +{8\cdot(x^2+y^2)^2} +{4a^2\cdot(2\cdot (x^3-3\,xy^2)-(x^2+y^2)\cdot (x^2+y^2+1))} -{8a^2\cdot(3\,x^2y-y^3)\cdot z} -{4\cdot (x^2+y^2)\cdot a^2z^2})^2=0
Kleeblattknoten 6
Lizenz CC BY-NC-SA-3.0

Formel
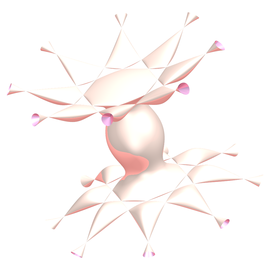
- x^18+9*x^16*y^2+36*x^14*y^4+84*x^12*y^6+126*x^10*y^8+126*x^8*y^10+84*x^6*y^12+36*x^4*y^14+9*x^2*y^16+y^18+4*x^16*z^2+32*x^14*y^2*z^2+112*x^12*y^4*z^2+224*x^10*y^6*z^2+280*x^8*y^8*z^2+224*x^6*y^10*z^2+112*x^4*y^12*z^2+32*x^2*y^14*z^2+4*y^16*z^2+6*x^14*z^4+42*x^12*y^2*z^4+126*x^10*y^4*z^4+210*x^8*y^6*z^4+210*x^6*y^8*z^4+126*x^4*y^10*z^4+42*x^2*y^12*z^4+6*y^14*z^4+4*x^12*z^6+24*x^10*y^2*z^6+60*x^8*y^4*z^6+80*x^6*y^6*z^6+60*x^4*y^8*z^6+24*x^2*y^10*z^6+4*y^12*z^6+x^10*z^8+5*x^8*y^2*z^8+10*x^6*y^4*z^8+10*x^4*y^6*z^8+5*x^2*y^8*z^8+y^10*z^8-40*x^14*y*z*a^2-120*x^12*y^3*z*a^2-8*x^10*y^5*z*a^2+360*x^8*y^7*z*a^2+520*x^6*y^9*z*a^2+280*x^4*y^11*z*a^2+40*x^2*y^13*z*a^2-8*y^15*z*a^2-80*x^12*y*z^3*a^2-160*x^10*y^3*z^3*a^2+144*x^8*y^5*z^3*a^2+576*x^6*y^7*z^3*a^2+464*x^4*y^9*z^3*a^2+96*x^2*y^11*z^3*a^2-16*y^13*z^3*a^2-40*x^10*y*z^5*a^2-40*x^8*y^3*z^5*a^2+112*x^6*y^5*z^5*a^2+176*x^4*y^7*z^5*a^2+56*x^2*y^9*z^5*a^2-8*y^11*z^5*a^2-2*x^14*a^4+86*x^12*y^2*a^4-242*x^10*y^4*a^4-330*x^8*y^6*a^4+330*x^6*y^8*a^4+242*x^4*y^10*a^4-86*x^2*y^12*a^4+2*y^14*a^4+12*x^12*z^2*a^4+272*x^10*y^2*z^2*a^4-420*x^8*y^4*z^2*a^4+320*x^6*y^6*z^2*a^4+900*x^4*y^8*z^2*a^4-80*x^2*y^10*z^2*a^4+20*y^12*z^2*a^4-2*x^10*z^4*a^4+90*x^8*y^2*z^4*a^4-420*x^6*y^4*z^4*a^4+420*x^4*y^6*z^4*a^4-90*x^2*y^8*z^4*a^4+2*y^10*z^4*a^4-40*x^10*y*z*a^6-40*x^8*y^3*z*a^6+112*x^6*y^5*z*a^6+176*x^4*y^7*z*a^6+56*x^2*y^9*z*a^6-8*y^11*z*a^6+x^10*a^8+5*x^8*y^2*a^8+10*x^6*y^4*a^8+10*x^4*y^6*a^8+5*x^2*y^8*a^8+y^10*a^8-4*x^16*b^2-32*x^14*y^2*b^2-112*x^12*y^4*b^2-224*x^10*y^6*b^2-280*x^8*y^8*b^2-224*x^6*y^10*b^2-112*x^4*y^12*b^2-32*x^2*y^14*b^2-4*y^16*b^2-12*x^14*z^2*b^2-84*x^12*y^2*z^2*b^2-252*x^10*y^4*z^2*b^2-420*x^8*y^6*z^2*b^2-420*x^6*y^8*z^2*b^2-252*x^4*y^10*z^2*b^2-84*x^2*y^12*z^2*b^2-12*y^14*z^2*b^2-12*x^12*z^4*b^2-72*x^10*y^2*z^4*b^2-180*x^8*y^4*z^4*b^2-240*x^6*y^6*z^4*b^2-180*x^4*y^8*z^4*b^2-72*x^2*y^10*z^4*b^2-12*y^12*z^4*b^2-4*x^10*z^6*b^2-20*x^8*y^2*z^6*b^2-40*x^6*y^4*z^6*b^2-40*x^4*y^6*z^6*b^2-20*x^2*y^8*z^6*b^2-4*y^10*z^6*b^2-4*x^14*a^2*b^2-28*x^12*y^2*a^2*b^2-84*x^10*y^4*a^2*b^2-140*x^8*y^6*a^2*b^2-140*x^6*y^8*a^2*b^2-84*x^4*y^10*a^2*b^2-28*x^2*y^12*a^2*b^2-4*y^14*a^2*b^2+80*x^12*y*z*a^2*b^2+160*x^10*y^3*z*a^2*b^2-144*x^8*y^5*z*a^2*b^2-576*x^6*y^7*z*a^2*b^2-464*x^4*y^9*z*a^2*b^2-96*x^2*y^11*z*a^2*b^2+16*y^13*z*a^2*b^2-8*x^12*z^2*a^2*b^2-48*x^10*y^2*z^2*a^2*b^2-120*x^8*y^4*z^2*a^2*b^2-160*x^6*y^6*z^2*a^2*b^2-120*x^4*y^8*z^2*a^2*b^2-48*x^2*y^10*z^2*a^2*b^2-8*y^12*z^2*a^2*b^2+80*x^10*y*z^3*a^2*b^2+80*x^8*y^3*z^3*a^2*b^2-224*x^6*y^5*z^3*a^2*b^2-352*x^4*y^7*z^3*a^2*b^2-112*x^2*y^9*z^3*a^2*b^2+16*y^11*z^3*a^2*b^2-4*x^10*z^4*a^2*b^2-20*x^8*y^2*z^4*a^2*b^2-40*x^6*y^4*z^4*a^2*b^2-40*x^4*y^6*z^4*a^2*b^2-20*x^2*y^8*z^4*a^2*b^2-4*y^10*z^4*a^2*b^2-4*x^12*a^4*b^2-24*x^10*y^2*a^4*b^2-60*x^8*y^4*a^4*b^2-80*x^6*y^6*a^4*b^2-60*x^4*y^8*a^4*b^2-24*x^2*y^10*a^4*b^2-4*y^12*a^4*b^2+80*x^10*y*z*a^4*b^2+80*x^8*y^3*z*a^4*b^2-224*x^6*y^5*z*a^4*b^2-352*x^4*y^7*z*a^4*b^2-112*x^2*y^9*z*a^4*b^2+16*y^11*z*a^4*b^2-4*x^10*z^2*a^4*b^2-20*x^8*y^2*z^2*a^4*b^2-40*x^6*y^4*z^2*a^4*b^2-40*x^4*y^6*z^2*a^4*b^2-20*x^2*y^8*z^2*a^4*b^2-4*y^10*z^2*a^4*b^2-4*x^10*a^6*b^2-20*x^8*y^2*a^6*b^2-40*x^6*y^4*a^6*b^2-40*x^4*y^6*a^6*b^2-20*x^2*y^8*a^6*b^2-4*y^10*a^6*b^2+6*x^14*b^4+42*x^12*y^2*b^4+126*x^10*y^4*b^4+210*x^8*y^6*b^4+210*x^6*y^8*b^4+126*x^4*y^10*b^4+42*x^2*y^12*b^4+6*y^14*b^4+12*x^12*z^2*b^4+72*x^10*y^2*z^2*b^4+180*x^8*y^4*z^2*b^4+240*x^6*y^6*z^2*b^4+180*x^4*y^8*z^2*b^4+72*x^2*y^10*z^2*b^4+12*y^12*z^2*b^4+6*x^10*z^4*b^4+30*x^8*y^2*z^4*b^4+60*x^6*y^4*z^4*b^4+60*x^4*y^6*z^4*b^4+30*x^2*y^8*z^4*b^4+6*y^10*z^4*b^4+8*x^12*a^2*b^4+48*x^10*y^2*a^2*b^4+120*x^8*y^4*a^2*b^4+160*x^6*y^6*a^2*b^4+120*x^4*y^8*a^2*b^4+48*x^2*y^10*a^2*b^4+8*y^12*a^2*b^4-40*x^10*y*z*a^2*b^4-40*x^8*y^3*z*a^2*b^4+112*x^6*y^5*z*a^2*b^4+176*x^4*y^7*z*a^2*b^4+56*x^2*y^9*z*a^2*b^4-8*y^11*z*a^2*b^4+8*x^10*z^2*a^2*b^4+40*x^8*y^2*z^2*a^2*b^4+80*x^6*y^4*z^2*a^2*b^4+80*x^4*y^6*z^2*a^2*b^4+40*x^2*y^8*z^2*a^2*b^4+8*y^10*z^2*a^2*b^4+6*x^10*a^4*b^4+30*x^8*y^2*a^4*b^4+60*x^6*y^4*a^4*b^4+60*x^4*y^6*a^4*b^4+30*x^2*y^8*a^4*b^4+6*y^10*a^4*b^4-4*x^12*b^6-24*x^10*y^2*b^6-60*x^8*y^4*b^6-80*x^6*y^6*b^6-60*x^4*y^8*b^6-24*x^2*y^10*b^6-4*y^12*b^6-4*x^10*z^2*b^6-20*x^8*y^2*z^2*b^6-40*x^6*y^4*z^2*b^6-40*x^4*y^6*z^2*b^6-20*x^2*y^8*z^2*b^6-4*y^10*z^2*b^6-4*x^10*a^2*b^6-20*x^8*y^2*a^2*b^6-40*x^6*y^4*a^2*b^6-40*x^4*y^6*a^2*b^6-20*x^2*y^8*a^2*b^6-4*y^10*a^2*b^6+x^10*b^8+5*x^8*y^2*b^8+10*x^6*y^4*b^8+10*x^4*y^6*b^8+5*x^2*y^8*b^8+y^10*b^8-8*x^15*a^2+40*x^13*y^2*a^2+280*x^11*y^4*a^2+520*x^9*y^6*a^2+360*x^7*y^8*a^2-8*x^5*y^10*a^2-120*x^3*y^12*a^2-40*x*y^14*a^2+16*x^13*z^2*a^2-96*x^11*y^2*z^2*a^2-464*x^9*y^4*z^2*a^2-576*x^7*y^6*z^2*a^2-144*x^5*y^8*z^2*a^2+160*x^3*y^10*z^2*a^2+80*x*y^12*z^2*a^2+24*x^11*z^4*a^2-168*x^9*y^2*z^4*a^2-528*x^7*y^4*z^4*a^2-336*x^5*y^6*z^4*a^2+120*x^3*y^8*z^4*a^2+120*x*y^10*z^4*a^2-80*x^11*y*z*a^4+880*x^9*y^3*z*a^4-1056*x^7*y^5*z*a^4-1056*x^5*y^7*z*a^4+880*x^3*y^9*z*a^4-80*x*y^11*z*a^4-80*x^9*y*z^3*a^4+960*x^7*y^3*z^3*a^4-2016*x^5*y^5*z^3*a^4+960*x^3*y^7*z^3*a^4-80*x*y^9*z^3*a^4+8*x^11*a^6-56*x^9*y^2*a^6-176*x^7*y^4*a^6-112*x^5*y^6*a^6+40*x^3*y^8*a^6+40*x*y^10*a^6-32*x^11*z^2*a^2*b^2+224*x^9*y^2*z^2*a^2*b^2+704*x^7*y^4*z^2*a^2*b^2+448*x^5*y^6*z^2*a^2*b^2-160*x^3*y^8*z^2*a^2*b^2-160*x*y^10*z^2*a^2*b^2-16*x^11*a^4*b^2+112*x^9*y^2*a^4*b^2+352*x^7*y^4*a^4*b^2+224*x^5*y^6*a^4*b^2-80*x^3*y^8*a^4*b^2-80*x*y^10*a^4*b^2+8*x^11*a^2*b^4-56*x^9*y^2*a^2*b^4-176*x^7*y^4*a^2*b^4-112*x^5*y^6*a^2*b^4+40*x^3*y^8*a^2*b^4+40*x*y^10*a^2*b^4-4*x^16-32*x^14*y^2-112*x^12*y^4-224*x^10*y^6-280*x^8*y^8-224*x^6*y^10-112*x^4*y^12-32*x^2*y^14-4*y^16-4*x^14*z^2-28*x^12*y^2*z^2-84*x^10*y^4*z^2-140*x^8*y^6*z^2-140*x^6*y^8*z^2-84*x^4*y^10*z^2-28*x^2*y^12*z^2-4*y^14*z^2+4*x^12*z^4+24*x^10*y^2*z^4+60*x^8*y^4*z^4+80*x^6*y^6*z^4+60*x^4*y^8*z^4+24*x^2*y^10*z^4+4*y^12*z^4+4*x^10*z^6+20*x^8*y^2*z^6+40*x^6*y^4*z^6+40*x^4*y^6*z^6+20*x^2*y^8*z^6+4*y^10*z^6-80*x^12*y*z*a^2-160*x^10*y^3*z*a^2+144*x^8*y^5*z*a^2+576*x^6*y^7*z*a^2+464*x^4*y^9*z*a^2+96*x^2*y^11*z*a^2-16*y^13*z*a^2+80*x^10*y*z^3*a^2+80*x^8*y^3*z^3*a^2-224*x^6*y^5*z^3*a^2-352*x^4*y^7*z^3*a^2-112*x^2*y^9*z^3*a^2+16*y^11*z^3*a^2+20*x^12*a^4-80*x^10*y^2*a^4+900*x^8*y^4*a^4+320*x^6*y^6*a^4-420*x^4*y^8*a^4+272*x^2*y^10*a^4+12*y^12*a^4+12*x^10*z^2*a^4-540*x^8*y^2*z^2*a^4+2520*x^6*y^4*z^2*a^4-2520*x^4*y^6*z^2*a^4+540*x^2*y^8*z^2*a^4-12*y^10*z^2*a^4+4*x^14*b^2+28*x^12*y^2*b^2+84*x^10*y^4*b^2+140*x^8*y^6*b^2+140*x^6*y^8*b^2+84*x^4*y^10*b^2+28*x^2*y^12*b^2+4*y^14*b^2-8*x^12*z^2*b^2-48*x^10*y^2*z^2*b^2-120*x^8*y^4*z^2*b^2-160*x^6*y^6*z^2*b^2-120*x^4*y^8*z^2*b^2-48*x^2*y^10*z^2*b^2-8*y^12*z^2*b^2-12*x^10*z^4*b^2-60*x^8*y^2*z^4*b^2-120*x^6*y^4*z^4*b^2-120*x^4*y^6*z^4*b^2-60*x^2*y^8*z^4*b^2-12*y^10*z^4*b^2-24*x^12*a^2*b^2-144*x^10*y^2*a^2*b^2-360*x^8*y^4*a^2*b^2-480*x^6*y^6*a^2*b^2-360*x^4*y^8*a^2*b^2-144*x^2*y^10*a^2*b^2-24*y^12*a^2*b^2-80*x^10*y*z*a^2*b^2-80*x^8*y^3*z*a^2*b^2+224*x^6*y^5*z*a^2*b^2+352*x^4*y^7*z*a^2*b^2+112*x^2*y^9*z*a^2*b^2-16*y^11*z*a^2*b^2-8*x^10*z^2*a^2*b^2-40*x^8*y^2*z^2*a^2*b^2-80*x^6*y^4*z^2*a^2*b^2-80*x^4*y^6*z^2*a^2*b^2-40*x^2*y^8*z^2*a^2*b^2-8*y^10*z^2*a^2*b^2-4*x^10*a^4*b^2-20*x^8*y^2*a^4*b^2-40*x^6*y^4*a^4*b^2-40*x^4*y^6*a^4*b^2-20*x^2*y^8*a^4*b^2-4*y^10*a^4*b^2+4*x^12*b^4+24*x^10*y^2*b^4+60*x^8*y^4*b^4+80*x^6*y^6*b^4+60*x^4*y^8*b^4+24*x^2*y^10*b^4+4*y^12*b^4+12*x^10*z^2*b^4+60*x^8*y^2*z^2*b^4+120*x^6*y^4*z^2*b^4+120*x^4*y^6*z^2*b^4+60*x^2*y^8*z^2*b^4+12*y^10*z^2*b^4+8*x^10*a^2*b^4+40*x^8*y^2*a^2*b^4+80*x^6*y^4*a^2*b^4+80*x^4*y^6*a^2*b^4+40*x^2*y^8*a^2*b^4+8*y^10*a^2*b^4-4*x^10*b^6-20*x^8*y^2*b^6-40*x^6*y^4*b^6-40*x^4*y^6*b^6-20*x^2*y^8*b^6-4*y^10*b^6+16*x^13*a^2-96*x^11*y^2*a^2-464*x^9*y^4*a^2-576*x^7*y^6*a^2-144*x^5*y^8*a^2+160*x^3*y^10*a^2+80*x*y^12*a^2+16*x^11*z^2*a^2-112*x^9*y^2*z^2*a^2-352*x^7*y^4*z^2*a^2-224*x^5*y^6*z^2*a^2+80*x^3*y^8*z^2*a^2+80*x*y^10*z^2*a^2+80*x^9*y*z*a^4-960*x^7*y^3*z*a^4+2016*x^5*y^5*z*a^4-960*x^3*y^7*z*a^4+80*x*y^9*z*a^4+6*x^14+42*x^12*y^2+126*x^10*y^4+210*x^8*y^6+210*x^6*y^8+126*x^4*y^10+42*x^2*y^12+6*y^14-4*x^12*z^2-24*x^10*y^2*z^2-60*x^8*y^4*z^2-80*x^6*y^6*z^2-60*x^4*y^8*z^2-24*x^2*y^10*z^2-4*y^12*z^2+6*x^10*z^4+30*x^8*y^2*z^4+60*x^6*y^4*z^4+60*x^4*y^6*z^4+30*x^2*y^8*z^4+6*y^10*z^4+120*x^10*y*z*a^2+120*x^8*y^3*z*a^2-336*x^6*y^5*z*a^2-528*x^4*y^7*z*a^2-168*x^2*y^9*z*a^2+24*y^11*z*a^2-2*x^10*a^4+90*x^8*y^2*a^4-420*x^6*y^4*a^4+420*x^4*y^6*a^4-90*x^2*y^8*a^4+2*y^10*a^4+4*x^12*b^2+24*x^10*y^2*b^2+60*x^8*y^4*b^2+80*x^6*y^6*b^2+60*x^4*y^8*b^2+24*x^2*y^10*b^2+4*y^12*b^2-12*x^10*z^2*b^2-60*x^8*y^2*z^2*b^2-120*x^6*y^4*z^2*b^2-120*x^4*y^6*z^2*b^2-60*x^2*y^8*z^2*b^2-12*y^10*z^2*b^2-4*x^10*a^2*b^2-20*x^8*y^2*a^2*b^2-40*x^6*y^4*a^2*b^2-40*x^4*y^6*a^2*b^2-20*x^2*y^8*a^2*b^2-4*y^10*a^2*b^2+6*x^10*b^4+30*x^8*y^2*b^4+60*x^6*y^4*b^4+60*x^4*y^6*b^4+30*x^2*y^8*b^4+6*y^10*b^4-8*x^11*a^2+56*x^9*y^2*a^2+176*x^7*y^4*a^2+112*x^5*y^6*a^2-40*x^3*y^8*a^2-40*x*y^10*a^2-4*x^12-24*x^10*y^2-60*x^8*y^4-80*x^6*y^6-60*x^4*y^8-24*x^2*y^10-4*y^12+4*x^10*z^2+20*x^8*y^2*z^2+40*x^6*y^4*z^2+40*x^4*y^6*z^2+20*x^2*y^8*z^2+4*y^10*z^2-4*x^10*b^2-20*x^8*y^2*b^2-40*x^6*y^4*b^2-40*x^4*y^6*b^2-20*x^2*y^8*b^2-4*y^10*b^2+x^10+5*x^8*y^2+10*x^6*y^4+10*x^4*y^6+5*x^2*y^8+y^10 +0.0001=0
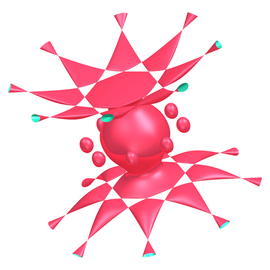
(2,5)-Torusknoten
Lizenz CC BY-NC-SA-3.0