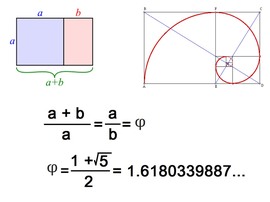
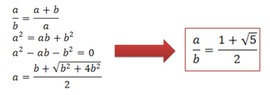
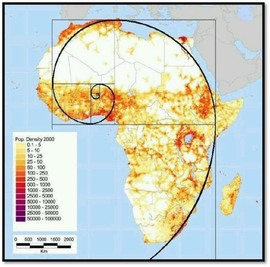
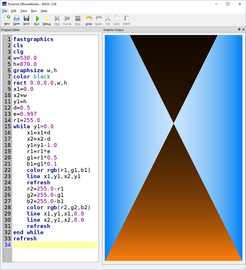
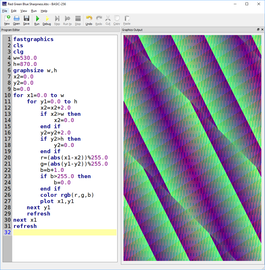
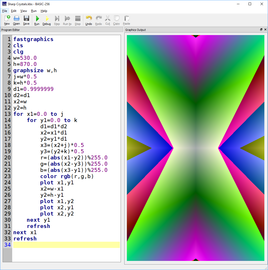
Jean Constant - Set theory
Georg Cantor (1845-1918) established the principle of set theory. It has become a fundamental theory in mathematics and is a powerful tool in topology, abstract algebra, and discrete mathematics.
The following two examples are part of a 21 plate series on the Cantor set theory available on Jean’s website. A technical, detailed description of the visualization process in available in the Springer proceedings of the Paris - 2010, Mathematics and Modern Art conference.

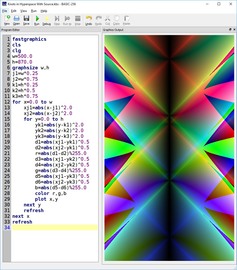
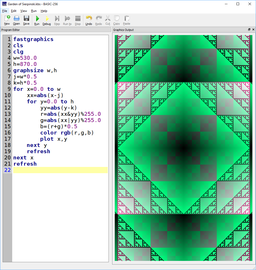
Cantor set theory #1
For this illustration, I created a background that would be the equivalent of the fractal plane first described by Wacław Sierpinski in 1916 as a generalization of the Cantor set. The resulting image is a series of 1 mm squares expanded 8 times.
Elements of optical illusions (in this example: the Hermann grid) were incorporated in the design to break the mechanical and repetitive aspect of the pattern expansion.
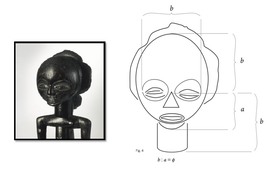
The Peruvian mask was added as an external element to link the composition into a larger cultural context.

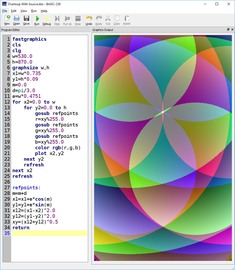
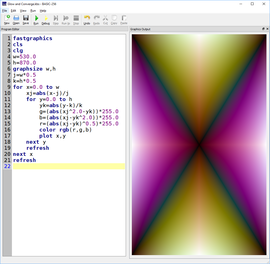
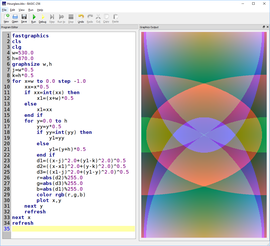
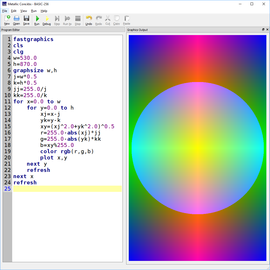
Cantor set theory #1
Following on the previous example that incorporated the Hermann grid and other elements of optical illusion techniques, I transformed the background original squares into monochromatic circles.
I added simple schematics of the Sierpinski grid as a reference in an opposite color scheme.
The final composition may remind some of the optical hypnotic effect staring at a Pachinko game.