Hand made hands-on
The hands-on objects which are presented here are an assortment of three exhibitions shown in Nuremberg, Germany, under the German titles, Form & Formel (2008), Keplers Formen (2009), and Die quasiperiodischen Formen (2011).
All objects are designed and created by Uli Gaenshirt, who also provided idea and concept for the exhibitions which were realized in voluntary collaboration with the KOMM-Bildungsbereich.
Spatial Pythagorean Model
A triangle with an edge lengths ratio 3:4:5 is rectangular because 3^2 + 4^2 = 5^2 fulfills the Pythagorean equation a^2 + b^2 = c^2 (Please note that x^2 signifies the second power of x).
The white object in the background is a downscaled model of the King’s Chamber in the Khufu Pyramid. Surprisingly, the red 3-4-5-triangle, a 12-knot drawstring, can be perfectly inscribed in the inside space.
The object in the foreground is a Spatial Pythagorean Stick Model. At the fixed vertical bar three marbles are countersunk, in the height of 7 units (red), 8 units (green) and 9 units (blue). Some complements are countersunk into the plane with respect to the possible integer Pythagorean solutions. The provided sticks with marked units have the lengths of integer diagonals.
In a spatial Cartesian coordinate system the distance d between a point P0 (0,0,0) and another point P1 (x,y,z) is given by the equation x^2 + y^2 + z^2 = d^2.
In accordance to the equation 12^2 + 20^2 + 9^2 = 25^2 the girl choosed the right stick to join the two blue marbles.
Pantheon Pythagorean Sphere Model
The young man is moving the bow of the Pythagorean Sphere Model. In doing so the inlayed black line segment of a circle circumscribes a sphere with radius 65 cm.
The corners of the wooden cuboids which can be contacted by the black line are integer solutions of the equation x^2 + y^2 + z^2 = 65^2. Actually the corner P (15|36|52) is touched.
On the whole sphere with radius 65 we can find 342 points with integer coordinates.
The influence behind this model is the Roman Pantheon (c. 120 AD). This is motivated on the one hand by the sphere which could be perfectly inscribed in the inside space, and on the other hand by the pattern on the floor, where 89 squares are fitted into the circular ground view, touching the circle in 16 corners. The design is based on the covering of two rectangles consisting of 11 x 3 squares and two others with 7 x 9 squares. All rectangles have the same diagonal length given by the Pythagorean equation 11^2 + 3^2 = 7^2 + 9^2.
Geometry of the Khufu (Cheops) Pyramid
The edges of the pyramid are streched by red drawstrings. The black triangle gives the slope of the pyramid faces. The ratio of the horizontal edge of the triangle, a, to its vertical edge, b, is 11:14. The value for a is commonly specified by 115.19 m, the length of 220 Egyptian royal cubits. The result for the height b is 146.60 m, resp. 280 royal cubits.
The model shows the geometric way to construct the almost identical heights b(τ) with the golden ratio τ (τ = 1.61803…) and b(π) with the circular constant π (π = 3.14159…).
b(τ) = (τ^0.5) a = 146.52 m
b(π) = 4 (π^-1) a = 146.66 m
(please note: τ^0.5 = √τ and: π^-1 = 1/π )
The ancient methods of measurement were not accurate enough to find a difference between b, b(τ) and b(π). Perhaps this is why the pyramid was regarded as a fundamental geometric construction.
Catenary and Parabola
The shape of the natural sag of a chain is called a catenary. The algebraic description of this curve corresponds to the addition of two hyperbolas, y = 0.5 e^x and y = 0.5 e^-x, which are specified by mirror reflection relative to the y-axe (e = 2.71828…).
If we fix, like in a rope bridge, identical weights with equidistant vertical drawstrings at a drawstring catenary, then the shape of the catenary will be transformed to the more cuspidal shape of a parabola.
The transformation can be easily understood realizing the more closed distribution of the attach points alongside the drawstring curve in its middle part in relation to the outer parts. The resulting higher weight in the midst gives the reason for the more cuspidal shape there, the lower weights in the outer parts induce the more streched shape of the drawstring curve relative to the chain which has a uniform weight.
Elliptic mechanics
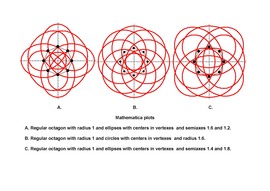
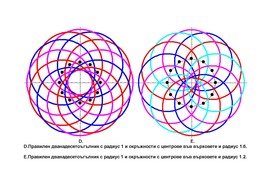
I. Viewed from the observation hole which is marked with the iron ring, the white ellipse fulfills exactly the black circle on the plexiglass window, i. e., the observation hole and the circle define a cone, with the ellipse as a cone section.
II. Johannes Kepler (1571-1630) constructed an ellipse on the base of intersection points given by the radius lines of two concentric circles. A horizontal straight line from the inner intersection point and a vertical straight line from the outer intersection point gives a cross-over point. Stringed together, these points are generating the ellipse. Please compare the crossing drawstrings in the upper left.
III: Using examples of points with integer coordinates it can be shown that the ellipse is a (horizontal) dilation of a circle.
IV. The ellipsograph, a stick movable on rectangularly mounted gliding channels, generates the same ellipse as a drawstring which is fixed in the focal points of the ellipse.
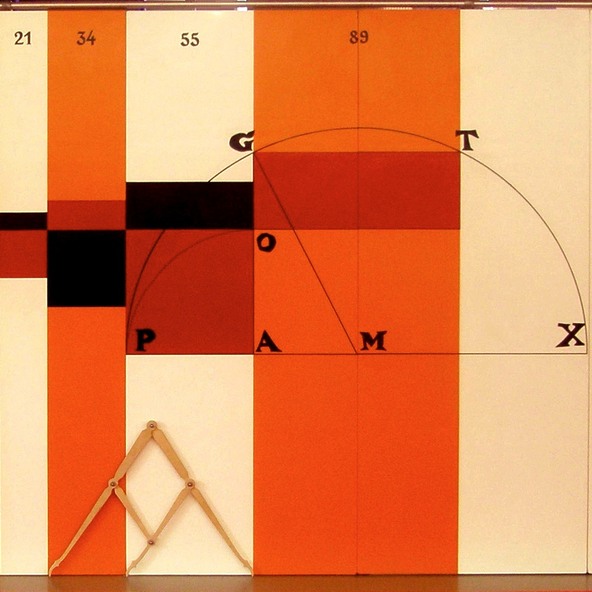
Kepler's ways to the Golden Ratio
The black outlined drawing, a woodcut of Johannes Kepler, shows how to generate the golden ratio, OA:GO = GA:OA, on the base of a rectangular triangle GAM with GA = 2 AM. In relation to the drawing the square AOP and the rectangle GOT have exactly the same areas.
Today, the golden ratio is commonly defined by: τ = 0.5 (√5+1) = 1,6180339887… .
Please note: OA:GO = GA:OA = τ.
The series expansion of squares and rectangles which is superposed to Keplers woodcut is based on the Fibonacci numbers F, with Fn+2 = Fn+1 + Fn , with F0 = 0 and F1 = 1 (i. e.: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, …). Kepler’s equation Fn+1 · Fn+1 = Fn · Fn+2 + (-1)^n consequently leads to: Fn+1 : Fn = τ, if lim n → ∞. With n = 9, the accordance of the area of the big red square (3025 cm^2 = 55 cm · 55 cm) to the area of the big red rectangle (3026 cm^2 = 34 cm · 89 cm) is nearly as perfect as in the accurate circle construction.
With the wooden proportional dividers the approximation of the golden ratio can be proved.
Icosahedral Mirrors with inlaid Hexagon
This mirror object, in which an inlaid hexagon appears 20 times, is very popular among children and adults.
The object consists of three mirrors in the form of isosceles triangles with a base-to-height ratio of 1: 0.5 τ (τ = 0.5 (√5 + 1) = 1.61803 …). This mirror object is made of wood.
The three mirrors are joined together at their thighs so that they enclose a 72° angle. Therefore, the black stripes attached to the hexagons appear as black pentagons. There are also many other depositors available.
Some of the objects from this gallery are documented in detail in the exhibition “IMAGINARY - Form und Formel mathematischer Fantasie”, which was shown for the first time in Nuremberg in June 2016.
(www. imaginary.org/event/imaginary-in-nuremberg)
Substitution and Projection
This object shows two different ways to generate a non periodic resp. quasiperiodic sequence on the base of the golden ratio τ, with τ = 0.5 (√5 + 1) = 1.61803… .
In the upper bar the substitution method is shown. In the first row of the bar the long blue interval Lq and the short orange interval Sq are in the ratio τ : 1. In the second row the intervals Lq and Sq are substituted by smaller copies: Lq → L + S + L + S + L and Sq → L + S + L, with L = Lq · τ^-3 and S = Sq · τ^-3 (please note: τ^-3 = 1 / τ^3 = 0.236…). The intervals L’ and S’ of the iterated substitution in the third row are again scaled down with the factor τ^-3.
An alternative way to generate a quasiperiodic sequence is the stripe projection method. The slope angle φ of the squared point lattice on the yellow board is given by tan φ = τ . The vertical projection of all points laying inside the red resp. in the orange horizontal stripes correspond perfectly to the sequences generated by the substitution method.
Fibonacci's Rabbits controlled by Quasi-Cells
In the early 13th century Leonardo Fibonacci described a hypothetical rule to calculate the growth of a rabbit population. This rule generates a quasiperiodic sequence of young and adult rabbit pairs. Attaching the length S to the young pairs, and the length L to the adult pairs, the sequence corresponds perfectly to that one which is generated by the substitution method.
The one dimensional (1D) quasi-cells in the upper part of the image generate the quasiperiodic sequence step by step. The successive growth is forced by sliding rulers (yellow). The rulers have a periodic average length. By connecting their end-marks, as shown in the image, the mechanisms of the quasi-cells force the growth of a perfect quasiperiodic sequence.
The 1D quasi-cells give the base for modelling flawless decagonal quasicrystalline growth by the algorithm of Quasiperiodic Succession. Detailed descriptions you will find in the files of the gallery Quasicrystalline Wickerwork.
Cartwheel with Penrose Rhombs
The Ammann grid which is drawn on the blue decagon is based on a vertical Fibonacci sequence with horizantally extended borderlines. This one-dimensional grid is asymetrically superposed by four copies of itself which are rotated by multiples of 36°.
The thick white and the small yellowish Penrose rhombs, which are magnetically fixed in the decagon center, are marked with specified cuts of the Ammann grid. The matching rules of the Penrose rhombs force the continuation of these lines from rhombus to rhombus.
A Penrose tiling is called a cartwheel if the marks of the rhombs are correlating to the Ammann grid of the decagon. The two black outlined rhombs in the upper part fulfill the matching rules but they do not correspond to the cartwheel order. It can be shown that a tiling which is freely puzzled out will finally lead to violations of the matching rules. The black outlined rhombs in the lower part are violating the matching rules.
Quasi-Cell Q
For modelling growth of quasicrystals neither the matching rules of the Penrose rhombs nor the related covering rules of alternative overlapping unit-cells (Gummelt decagons) are strong enough to avoid mismatches.
The algorithm of the quasiperiodic succession also works step-by-step but it generates the growth of a flawless cartwheel order controlling each thick rhombus by a quasi-cell Q.
A quasi-cell Q has five sliding rulers with a periodic average length (yellow). The rulers of the start-cell have a starlike position. The big blue quasi-cell Q is related to the blue rhombus of the cartwheel order in the upper left. In this cell only one ruler is shown, movably guided on the respective red twin scale. The position of this ruler depends from the correlation with the parallel ruler of the start-cell in the lower left. Its end mark on the right allows to impart its position to the (not shown) ruler of the parallel green scale of the suivel-mounted black outlined plexiglass rhombus in the upper right. Its position is related to the green rhombus of the cartwheel order in the upper left.
Detail of the Quasi-Cell Q
In this detailed view of the cell Q the position of the plexiglass rhombus is different relative to the position in the predecessor image. The white arrow shows in which way the rhombus has been rotated about 144°. However, both positions are in accordance to the matching rules because the continuation of the Ammann lines is warranted in each case.
In the predecessor image the end mark on the right hand side of the ruler could be connected with the (not shown) ruler of the parallel green scale because both end marks stood inside the common interval of the parallel scales marked by the yellow bracket.
In the alternative rhombus position which is shown in the adjacent image the end mark stands outside the common interval which is marked by the shorter yellow bracket. Therefore this rhombus position is not allowed at this place relative to the start-cell. The quasiperiodic succession algorithm solely determines positions which correspond to a perfect cartwheel order. The definition of the cartwheel order is unambiguous and reaches towards infinity.
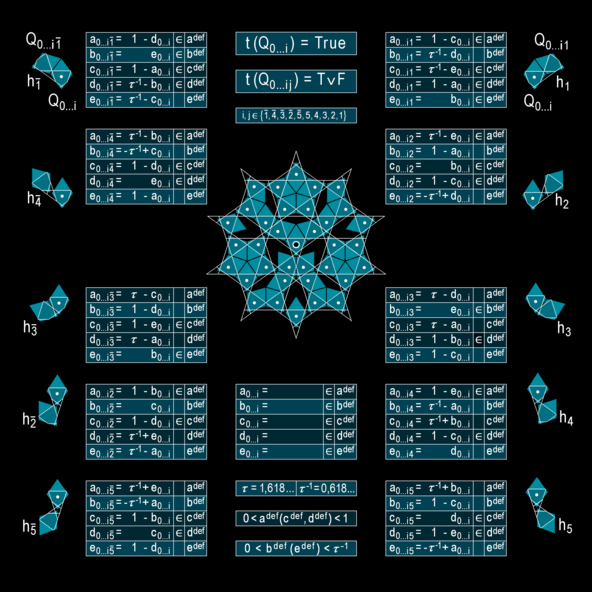
Algorithm of Decagonal Quasiperiodic Succession
The recursive formula consists of 50 scale value equations. The ten blocks in the outer columns correspond to the ten possible rhombus neighborhoods hj which are shown beside the columns. a, b, c, d and e are the values of the five double scales of a quasicell Q. The double scales are rotated by 36° to one another. Each thick rhombus can be assigned a quasicell Q.
The five values of the start cell Q0 are infinitesimally small, i. e. μ0 = 10^–n, with lim n → ∞. If they are entered in the central block, the formula leads to four valid neighbours, h1*, h2*, h4 and h1 (because their five respective values are valid) and six invalid neighbours (because one or more of their respective values are invalid). Please note that an asterisk is used here instead of an overline to indicate an inverse operation.
The valid values of Q01*, Q02*, Q04 and Q01are entered in the central block of four new formula sheets whereby the next generation of neighbours can be calculated. This recursiv scheme creates step by step an error-free quasiperiodic cartwheel order, as required for such a growth model.