The Mandelbox in PseudoKleinian grid
An advanced way to integrate particular Mandelbox parameters in PseudoKleinian order and somewhere beyond.
Definition: Similar to the relation of the Mandelbrot set and the Julia sets I will talk about the M-set and J-sets in connection with the Mandelbox and the PseudoKleinian. This is to avoid name confusion.
This is just a proof of concept. A formal analysis is not part of this elaboration. In the final stage I placed a particular Mandelbox
J-set at the end of a four formula cycle. That’s all.
Mathematically, there is nothing significantly new here. The transformations come from the standard repertoire of today’s
software – Mandelbulber in this case. Only the combination is new. From an artistic point of view, it is a nice to have gadget, that also emphasises the modular character of this type of 3D fractal.
parameters for Mandelbulber 2
The parameters are made with version 2.32 of Mandelbulber. Earlier versions won’t open theese without manual editing. And I do not recommend that. Use the parameters at your own risk.
How to import parameters in Mandelbulber
Method 1: Mostly your browser will open the text file in your browser window. Select the complete text and copy to clipboard. Open Mandelbulber and choose >file >Load settings from clipboard… Hit render in main window
Method 2: rightclick the link to parameters >save link as txt-file. Open Mandelbulber and choose >file >Load settings… Mandelbulber opens *.txt as well as *.fract files
>>WIP
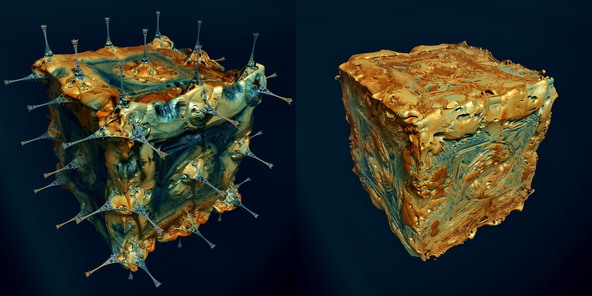
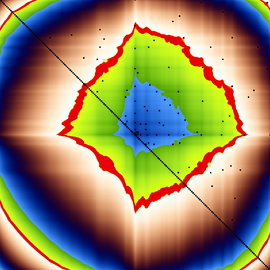
The M-set
The figure shows the M-set of a Mandelbox with negative scale and rotated folding planes (negscale rotbox) – with (l) and without (r) grid-Mandelbox.
The grid-Mandelbox means: scale=1 (neutral) minRadius=0, the rest default and this 12-20 times – this depends on other parameters – and without adding c. For further info see attached parameters.
>> the parameters were replaced due to an error (10/06)
We see a Mandelbox that is deformed but unchanged in overall size. At this point, I was not sure, whether this is a simple overlay or a completely new object. It turned out to be an overlay. What do I mean?
You can implant a particular Mandelbox J-set parameter with all the trimmings (including the global constant c) and the result shows this Mandelbox in many precise details, woven in a PseudoKleinian grid. The grid Mandelbox has no influence on detail development
the harvest
the harvest – more or less a classic from 2011. I used this as input parameter. Clear shapes. Suitable for that quest.
The parameters ar included in the gallery The Mandelbox, an artistic and geometric journey | IMAGINARY
Early plain
an early, plain implementation already shows many parts of the original parameter.
This is a two formula cycle. Mandelbox + Mandelbox in different configurations. Global c is added after the second one.
by modern means
one step further. Adding a linear offset between the two slots, makes it possible, to move the second Mandelbox within the PseudoKleinian grid. Yes, it is that simple.
sculpting with the mandelbox
A sphere inversion as pre transform (slot 1) completes the elaboration. With the resulting four slot system you can almost sculpt freely with the input parameter.
harvesting
Same overall environment as the previous one, only altering shere inversion and add constant parameters.
cocoon
And a third one with “the harvest” as input parameter. Also here only sphere inversion and add constant parameters are edited. Finding apt parameters is quite a quest. I “find” them by creating large random fields for the three dimensional vectors involved. This seems the most effective method to me. Mandelbulber has built in opportunities to exchange data of animations with spread sheets via csv-files. Here I simply generate random fields of any size.
modern nostalgy
A Mandelbox as shown in PIP in PseudoKleinian. The difference between a plain PseudoKleinian, which is Mandelbox+Mandelbox and this four slot cycle is sphere inversion and add constant, both executed one time. A non-linear and a linear transformation. I can imagine, that this combination is resposible for this “spiraling off”, for which I have no other explanation.
the guardian
This is an example of a randomly created result. Done with a basic, unrotated Mandelbox
sacrilege
Annoter one from a similar unrotated Mandelbox.
Parameter is a to do
