Ripple Weave
Galerie
Ripple Weave
Nested trigonometric functions mapped onto HSL space then drawn on a WebGL canvas. Rendered on my little custom program.

Formel
- f(a,b) = \mod(\tan(a-\sin(b\sin a)),\tfrac3a)
- hsl(x,y) = \begin{bmatrix} f(x,y)+0.8 \\ 0.4 \\ \min(\sqrt{f(x,y)},1) \end{bmatrix}
- zoom = e^{-3.3}
Bidents
Lizenz CC BY-NC-SA-3.0

Formel
- f(a,b) = \sin\frac a{\cos\frac b{\sin\frac a{\cos b}}}
- g(a,b) = f(e^a,e^b)
- hsl(x,y) = \begin{bmatrix} \frac{g(x,y)+1}2 \\ 1-g(x,y) \\ g(x,y) \end{bmatrix}
- zoom = e^{-2}
Silk
Lizenz CC BY-NC-SA-3.0

Formel
- f(a,b) = (\sin a)^{\tan\frac ab}
- hsl(x,y) = \begin{bmatrix} f(x,y) \\ 0.8 \\ f(y,x)-f(x,y) \end{bmatrix}
- zoom = e^{-1.1}
Windspinner
Lizenz CC BY-NC-SA-3.0

Formel
- f(a,b) = \left|\sin\frac{\arctan\frac ba}{\sin\sqrt{a^2+b^2}}\right|
- hsl(x,y) = \begin{bmatrix} \frac{f(xy,y^2)}{10} \\ f(x^2,xy)-1 \\ -\log f(xy,y^2) \end{bmatrix}
- zoom = e^{-2}
Turbine
Lizenz CC BY-NC-SA-3.0
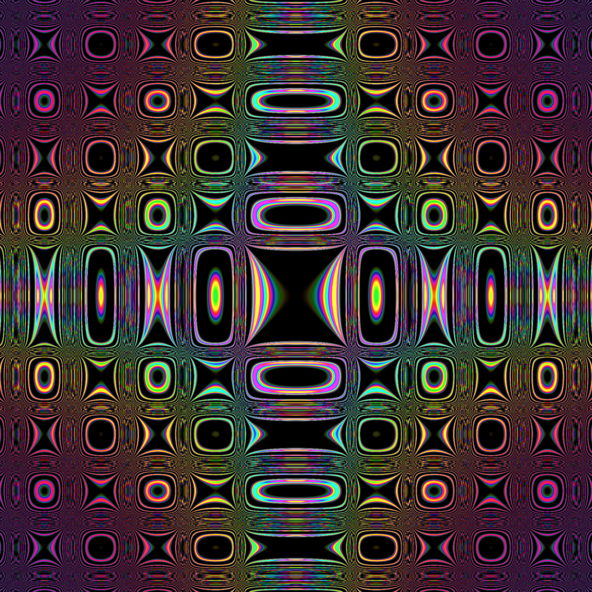
Formel
- f(a,b) = \sin\frac{\frac a{\sin a}-\frac b{\sin b}}{\frac{\log(a^2b^2+100)}{10}}
- hsl(x,y) = \begin{bmatrix}f(x,y) \\ 0.9 \\ f(x,y) \end{bmatrix}
- zoom = e^{-3}
Bismuth
Lizenz CC BY-NC-SA-3.0

Formel
- f(a,b)=\sin\frac{-\tan a}{\sin(\frac ba-\sin(\frac ab-\sin\frac ba)}
- hsl(x,y)=\begin{bmatrix}\frac{f(x,y)}2+0.2\\1-\min(\max(f(x^2,y),0),1)^4\\f(x^2,y)\end{bmatrix}
- zoom = e^{-2}
Butterfly
Lizenz CC BY-NC-SA-3.0