Jean-Francois Colonna - Number Theory
(Pictures of Number Theory)

The 126.646 first digits -base 6- of the square root of 2 displayed as a tridimensional random walk.
Each digit N -base 6- defines the current step of an “absolute” tridimensional random walk:
digit=0 ==> move(+D,0,0) digit=1 ==> move(-D,0,0) digit=2 ==> move(0,+D,0) digit=3 ==> move(0,-D,0) digit=4 ==> move(0,0,+D) digit=5 ==> move(0,0,-D)with D=1.
The 126.646 first digits -base 6- of the golden ratio displayed as a tridimensional random walk.
Each digit N -base 6- defines the current step of an “absolute” tridimensional random walk:
digit=0 ==> move(+D,0,0)digit=1 ==> move(-D,0,0)
digit=2 ==> move(0,+D,0)
digit=3 ==> move(0,-D,0)
digit=4 ==> move(0,0,+D)
digit=5 ==> move(0,0,-D)
with D=1.
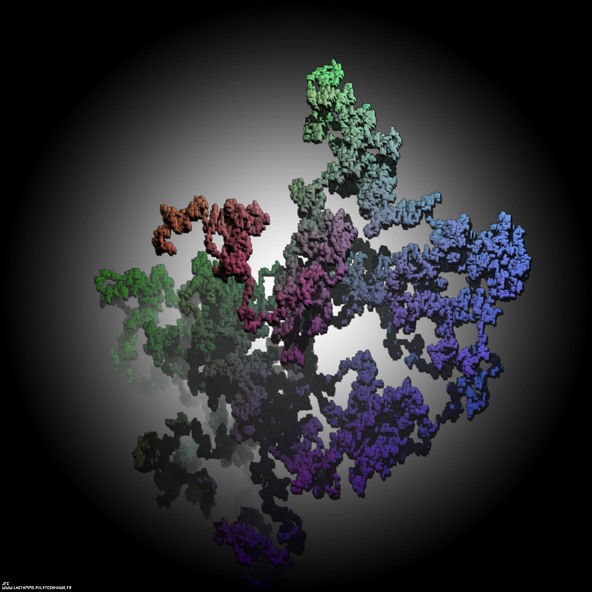
The 126.922 first digits -base 6- of 'e' displayed as a tridimensional random walk.
Each digit N -base 6- defines the current step of an “absolute” tridimensional random walk:
digit=0 ==> move(+D,0,0)digit=1 ==> move(-D,0,0)
digit=2 ==> move(0,+D,0)
digit=3 ==> move(0,-D,0)
digit=4 ==> move(0,0,+D)
digit=5 ==> move(0,0,-D)
with D=1.

The 126.646 first digits -base 6- of 'pi' - displayed as a tridimensional random walk.
Each digit N -base 6- defines the current step of an “absolute” tridimensional random walk:
digit=0 ==> move(+D,0,0)digit=1 ==> move(-D,0,0)
digit=2 ==> move(0,+D,0)
digit=3 ==> move(0,-D,0)
digit=4 ==> move(0,0,+D)
digit=5 ==> move(0,0,-D)
with D=1.
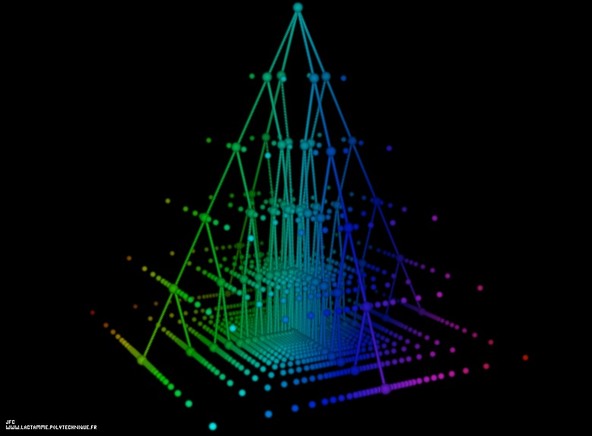
Generation of the 63x63 first Conway's surreal complex numbers

Tridimensional Hilbert Curve -iteration 4-.

A pseudo-periodical Penrose tiling of the Golden Decagon.
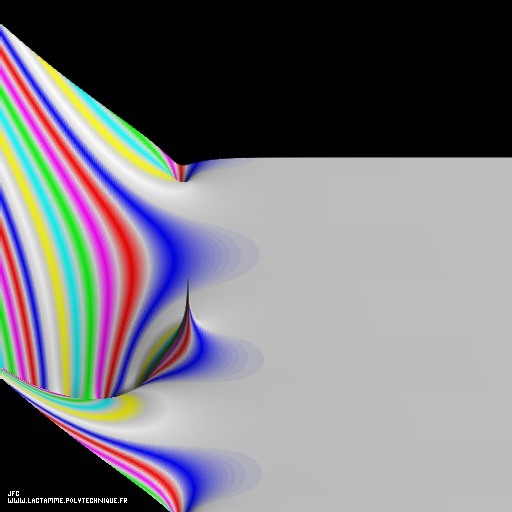
Tridimensional display of the Riemann Zeta function inside (-10.0,+20.0)x(-15.0,+15.0).

Tridimensional display of the Riemann Zeta function inside (+0.1,+0.9)x(0,+50).
Here is the meaning of the three {X,Y,Z} display coordinates:
X = Re(Zeta(z))Y = Im(Zeta(z))Z = Re(z)
The Goldbach conjecture -the Goldbach comet or the Goldbach rainbow- from 6 to 411678.
The Goldbach conjecturestates that each even integer number N greater or equal to 4 can be written as the sum of two prime numbers. For example:
4 = 2+2 6 = 3+3 8 = 3+5 [= 5+3] 10 = 3+7 = 5+5 [= 7+3] (…) 70 = 3+67 = 11+59 = 17+53 = 23+47 = 29+41 [= 41+29 = 47+23 = 53+17 = 59+11 = 67+3] (…) 990 = 7+983 = 13+977 = 19+971 = 23+967 = 37+953 = 43+947 = 53+937 = 61+929 = 71+919 = 79+911 = 83+907 = 103+887 = 107+883 = 109+881 = 113+877 = 127+863 = 131+859 = 137+853 = 151+839 = 163+827 = 167+823 = 179+811 = 181+809 = 193+797 = 229+761 = 233+757 = 239+751 = 251+739 = 257+733 = 263+727 = 271+719 = 281+709 = 307+683 = 313+677 = 317+673 = 331+659 = 337+653 = 347+643 = 349+641 = 359+631 = 373+617 = 383+607 = 389+601 = 397+593 = 419+571 = 421+569 = 433+557 = 443+547 = 449+541 = 467+523 = 487+503 = 491+499 [= 499+491 = 503+487 = 523+467 = 541+449 = 547+443 = 557+433 = 569+421 = 571+419 = 593+397 = 601+389 = 607+383 = 617+373 = 631+359 = 641+349 = 643+347 = 653+337 = 659+331 = 673+317 = 677+313 = 683+307 = 709+281 = 719+271 = 727+263 = 733+257 = 739+251 = 751+239 = 757+233 = 761+229 = 797+193 = 809+181 = 811+179 = 823+167 = 827+163 = 839+151 = 853+137 = 859+131 = 863+127 = 877+113 = 881+109 = 883+107 = 887+103 = 907+83 = 911+79 = 919+71 = 929+61 = 937+53 = 947+43 = 953+37 = 967+23 = 971+19 = 977+13 = 983+7] (…)The horizontal axis represents the even numbers N={6, 8, 10, 12,…} starting at 6 (for compatibility with the other related visualizations). The “altitude” of each point exhibits the number of decompositions of N as sums of two prime numbers.
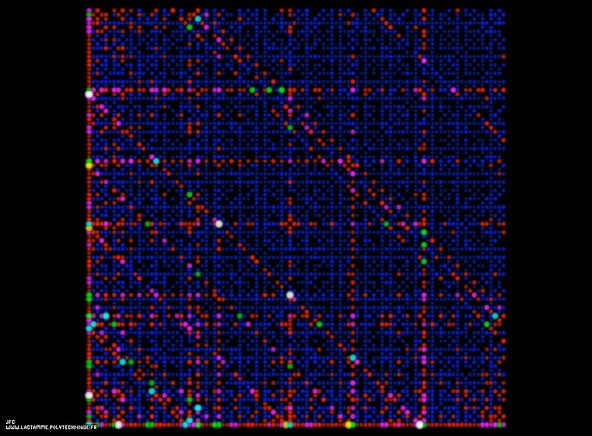
The ABC conjecture.
The horizontal and vertical axes display respectively two whole numbers A and B. Each disk display a couple of coprime numbers A and B:
GCD(A,B)=1The number C is the sum of A and B:
C = A+BThe function Radical(N) gives the product of the prime factors (with an exponent equals to 1) of N. For example:
N = 1960 = 2^3 .5^1 .7^2 Radical(1960) = 2^1 .5^1 .7^1 = 2.5.7 = 70Then the following function is computed:
k(A,B,C) = log(C) / log(Radical(A. B.C))The ABC conjecture states that k(A,B,C) is less than a certain constant (unknown, but greater than 1 and hopefully lesser than 2…) whatever the values of A and B.
The surface and the luminance of each disk are proportional to k(A,B,C).
For this picture, the numbers A and B belong to [1,100] giving birth to the following values:
min(k(A,B,C))=0.37117806024788 max(k(A,B,C))=1.22629438553090
The Syracuse conjecture -polar coordinates display-
The Syracuse sequence is defined as follows:
U(0) = N (an integer number)if U(n) is even :
U(n+1) = U(n)/2
else :
U(n+1) = 3.U(n) + 1
- The Syracuse conjecture states that sooner or later the {[[4,] 2,] 1} sequence will appear whatever the starting number N (and then repeats itself obviously ad vitam eternam). For example with N=7:
U(0) = 7 U(1) = 22 U(2) = 11 U(3) = 34 U(4) = 17 U(5) = 52 U(6) = 26 U(7) = 13 U(8) = 40 U(9) = 20 U(10) = 10 U(11) = 5 U(12) = 16 U(13) = 8 U(14) = 4 U(15) = 2 U(16) = 1
- This picture is a circular display of sixteen different sequences from U(0)=5 (lower left) to U(0)=20 (upper right). For each sequence U(n) the following “star” is generated:
Rho(n) = U(n) (with a renormalization inside [0,1])Teta(n) = 2.pi.n/(nm+1)X(n) = Rho(n).cos(Teta(n)) Y(n) = Rho(n).sin(Teta(n))where ‘nm’ denotes the maximal value of ‘n’:
U(nm) = 1The colors used are a function of ‘n’ (from Dark Blue [n=0] to White with an increasing luminance).

The additive persistence of the 65536 first integer numbers for the bases 2 -lower left- to 17 -upper right-.
Starting from the origin of the coordinates (at the center of the picture), one follows a square spiral-like path and numbers each integer point encountered (1, 2, 3,…).
Then one displays the N-th point with the false color f(PA(N,B)) where:
PA(N,B) = the additive persistence of N for the base B, f(…) = an arbitrary ascending functionLet’s define PA(N,B) with an obvious example:
B = 10 N = 856 (= 8xB^2 + 5xB^1 + 6xB^0)Then the following sequence is computed:
856 —-> (8+5+6) = 19 —-> (1+9) = 10 —-> (1+0) = 1It takes three (3) steps to reach a one digit number. Then:PA(856,10) = 3

The multiplicative persistence of the 65536 first integer numbers for the bases 2 -lower left- to 17 -upper right-.
Starting from the origin of the coordinates (at the center of the picture), one follows a square spiral-like path and numbers each integer point encountered (1, 2, 3,…).
Then one displays the N-th point with the false color f(PM(N,B)) where:
PM(N,B) = the multiplicative persistence of N for the base B, f(…) = an arbitrary ascending function.Let’s define PM(N,B) with an obvious example:
B = 10 N = 77 (= 7xB^1 + 7xB^0)Then the following sequence is computed:
77 —-> (7x7) = 49 —-> (4x9) = 36 —-> (3x6) = 18 —-> (1x8) = 8 It takes four (4) steps to reach a one digit number (by the way it is the longest sequence with a two digit number). Then:PM(77,10) = 4A conjecture states that PM(N,10) cannot exceed 11…
Here is an example of a longer sequence:48699984 —-> 4478976 —-> 338688 —-> 27648 —-> 2688 —-> 768 —-> 336 —-> 54 —-> 20 —-> 0

12 evenly distributed points on a sphere -an Icosahedron- by means of simulated annealing.
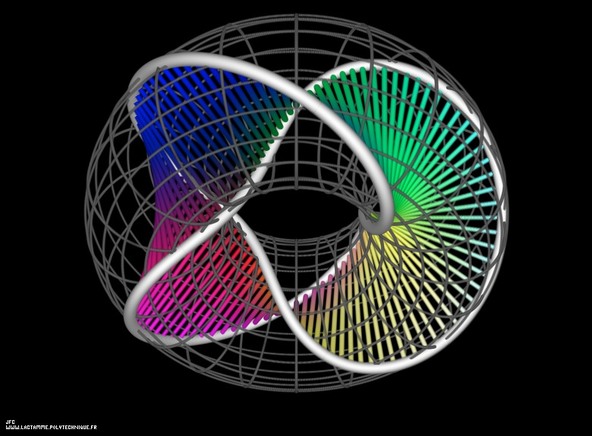
3-foil torus knot on its torus.

Three successive elementary monodimensional binary cellular automata -106,90,86- with 1 yellow starting point -bottom middle-.
An elementary monodimensional binary automaton is a monodimensional set of cells. At time ‘t’, each cell (with coordinate ‘x’) has a value ‘CELL(x,t)’ that equals either 0 (Black) or 1 (White) and has two neighbours (one at its left ‘CELL(x-1,t)’ and one at its right ‘CELL(x+1,t)’). The points outside the picture (at left and at right) are assumed to be White. The time evolution of this set of cells is defined by means of rules.
This picture was computed using successively the three following elementary monodimensional binary cellular automata:
automaton 86 (for t E [401,574]) -white background-
automaton 90 (for t E [101,400]) -light orange background-
automaton 106 (for t E [0,100]) -dark orange background-
The vertical axis is the time axis and the initial conditions are displayed on the bottom line.

Tridimensional display of the dynamics of the bidimensional John Conway's life game
The third coordinate ‘Z’ is the time ‘T’, whereas the two space coordinates X’ and ‘Y’ are periodical

The tridimensional John Conway's life game with random initial conditions -25% of occupied cells-.
The bidimensional life game was initially defined by Conway. It uses an empty square mesh (all vertices are turned off). At time t=0 some vertices are occupied (they are turned on): this is the initial state. To go from the time t to the time t+1, it suffices to count for each vertex -or “Cell”- C(x,y) the number N of its neighbours (it is less than or equal to 3^2-1=8) and then to possibly change the state of M according to the following bidimensional automata rules:
[R1 = Birth] ((C(t).IS.off).AND.(N == 3)) ==> C(t+1) on [R2 = Death] ((C(t).IS.on).AND.((N < 2).OR.(N > 3))) ==> C(t+1) off [R3] other cases ==> C(t+1)=C(t)The boundary conditions can be periodical or not.
This process can extended in a tridimensional space. The number N of neighbours of the vertex -or “Cell”- C(x,y,z) is computed (it is less than or equal to 3^3-1=26) and the preceding rules can be extended as follows:
[R1 = Birth] ((C(t).IS.off).AND.((N >= NB1).AND.(N <= NB2))) ==> C(t+1) on [R2 = Death] ((C(t).IS.on).AND.((N < ND1).OR.(N > ND2))) ==> C(t+1) off [R3] other cases ==> C(t+1)=C(t)The bidimensional and tridimensional processes can be extended one step further using two binary lists ‘LD’ and ‘LA’ (“Dead” -off- and “Alive” -on- respectively):
[R1 = Birth] ((C(t).IS.off).AND.(LD[N] == 1)) ==>C(t+1)=on [R2 = Death] ((C(t).IS.on).AND.(LA[N] == 1)) ==>C(t+1)=off [R3] other cases ==> C(t+1)=C(t)(“1” means “to change the state” and “0” means “the state is unchanged”).
For this picture, the parameters have the following values:
NB1=10 NB2=14 ND1=8 ND2=16
Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb') with a 1/O conformal transformation in the pseudo-octonionic space -tridimensional cross-section-.

Close-up on a pseudo-octonionic Mandelbrot set (a 'Mandelbulb') with a 1/O conformal transformation in the pseudo-octonionic space -tridimensional cross-section-.

The 64 first lines of the Pascal's Triangle.
The white peaks display the coefficients that are divisible by 2, 3, 5 and 7 (when the dark blue ones displays the coefficients that are not divisible by 2, 3, 5 and 7). The other colors display the other cases… The height of each point is proportional to the luminance of its color.
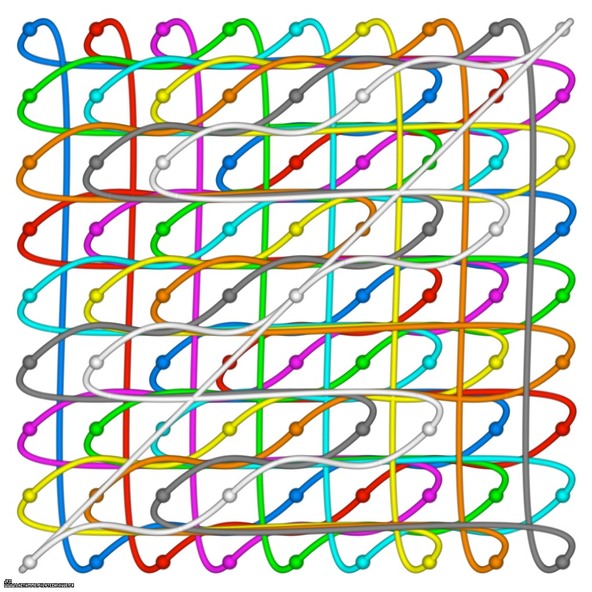
Artistic display of a Sudoku grid.
Here is the used grid with each digit (from 1 to 9) displayed with its own color:
1 2 3 | 4 5 6 | 7 8 9 4 5 6 | 7 8 9 | 1 2 3 7 8 9 | 1 2 3 | 4 5 6 ———+———-+——— 2 3 4 | 5 6 7 | 8 9 1 5 6 7 | 8 9 1 | 2 3 4 8 9 1 | 2 3 4 | 5 6 7 ———+———-+——— 3 4 5 | 6 7 8 | 9 1 2 6 7 8 | 9 1 2 | 3 4 5 9 1 2 | 3 4 5 | 6 7 8