Jean Constant - Conformal maps
Graphically, a conformal map transforms any pair of curves intersecting at a point in the region so that the image curves intersect at the same angle. (Driscoll.) Conformal maps can be defined between domains in higher dimensional Euclidean spaces and Riemannian manifold geometry.
Conformal mapping is extremely important in complex analysis, physics and engineering (Wolfram).
Two examples from a 16 plate portfolio on the conformal map function available at hermay.org

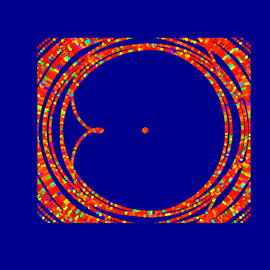
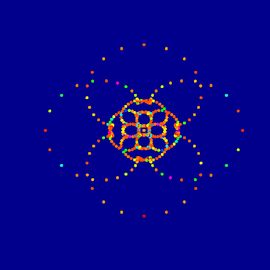
Eliptic function #1
The main object of the composition is a wireframe visualization of the elliptic function z —> Sine(z) created in Richard Palais’ 3D-XplorMath software.
The outline was manipulated and distorted in a raster graphic program in order to use the dynamic of the visualization to suggest a 3 & 4 dimension environment.
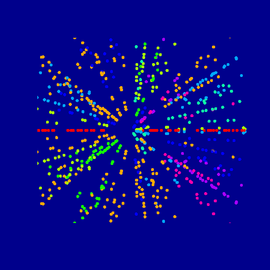
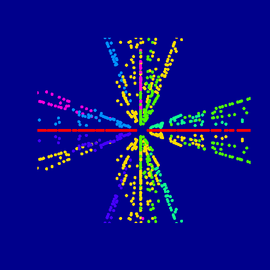
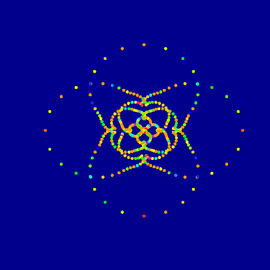
Eliptic function #2
Variation on the function z —> 1/z+z extracted in 3DXplorMath.
The wireframe pattern was imported in a raster graphic program. The shapes were manipulated and duplicated to give a mirror effect to the overall composition.