The Italian premiere of a large IMAGINARY exhibition
Oliver Labs
galería
Oliver Labs
Oliver Labs es un geómetra especialista en algoritmos y computación. Esto incluye la construcción de interesantes curvas y superficies, su visualización y el estudio de diversos problemas algorítmicos relacionados. Estas imágenes muestran superficies algebraicas con un sorprendente número de singularidades.
Fórmula
- P_6 − αK^2 = 0
- P_6 = ( τ^2x^2−y^2)( τ^2y^2−z^2)( τ^2z^2− x^2), τ = (1+\sqrt{5})/2
- α = (2τ+1)/4=(2+\sqrt{5})/4
- K = x^2+y^2+z^2−1
Séxtica de Barth
Los Guiness de las singularidades / Récord por sorpresa
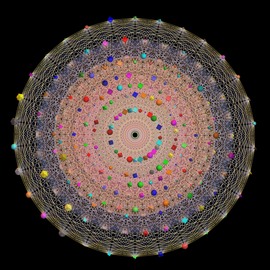
La séxtica de Barth es una superficie de grado seis construida en 1996 por Wolf Barth. Es remarcable porque contiene el máximo número de singularidades que pueden aparecer en un polinomio de grado seis, 65. ¡Pero esto no se demostró hasta 1997! Para muchos geómetras esto significó una gran sorpresa, puesto que ellos pensaban que el máximo era 64.
Existen diferentes familias de superficies con la propiedad de ser un polinomio de grado seis y tener 65 singularidades. Pero la séxtica de Barth destaca por su simetría en forma de icosaedro.
La forma de la séxtica de Barth recuerda a la de una molécula llamada fulereno. Dicha molécula es la tercera forma más estable del carbono, junto al grafito y al diamante, y se llama así en memoria de Buck-minster Fuller, el primer matemático-arquitecto en “imaginarse” esta forma.
Licencia CC BY-NC-SA-3.0
Fórmula
- x^7-21*x^5*y^2+35*x^3*y^4-7*x*y^6+7*x^6*1+21*x^4*y^2*1+21*x^2*y^4*1+7*y^6*1-57*x^4*1^3-114*x^2*y^2*1^3-57*y^4*1^3+(24/7*a^2+768/49*a+800/7)*x^2*1^5+(24/7*a^2+768/49*a+800/7)*y^2*1^5+(-149808/2401*a^2+3216/343*a-147584/2401)*1^7+(-49*a^2+7*a-52)*x^4*1^2*z+(-98*a^2+14*a-104)*x^2*y^2*1^2*z+(-49*a^2+7*a-52)*y^4*1^2*z+(128/7*a^2+704/49*a+128/7)*x^2*1^4*z+(128/7*a^2+704/49*a+128/7)*y^2*1^4*z+(-1632/343*a^2+16/7*a-192/343)*1^6*z+(-98*a^2+14*a-101)*x^4*1*z^2+(-196*a^2+28*a-202)*x^2*y^2*1*z^2+(-98*a^2+14*a-101)*y^4*1*z^2+(3016/7*a^2-2904/49*a+440)*x^2*1^3*z^2+(3016/7*a^2-2904/49*a+440)*y^2*1^3*z^2+(-17440/343*a^2+416/49*a-17040/343)*1^5*z^2+(-49*a^2+7*a-50)*x^4*z^3+(-98*a^2+14*a-100)*x^2*y^2*z^3+(-49*a^2+7*a-50)*y^4*z^3+(5776/7*a^2-5648/49*a+5888/7)*x^2*1^2*z^3+(5776/7*a^2-5648/49*a+5888/7)*y^2*1^2*z^3+(-313136/343*a^2+6288/49*a-319264/343)*1^4*z^3+(3680/7*a^2-3608/49*a+536)*x^2*1*z^4+(3680/7*a^2-3608/49*a+536)*y^2*1*z^4+(-592240/343*a^2+11856/49*a-603856/343)*1^3*z^4+(816/7*a^2-800/49*a+832/7)*x^2*z^5+(816/7*a^2-800/49*a+832/7)*y^2*z^5+(-458832/343*a^2+1312/7*a-467840/343)*1^2*z^5+(-166272/343*a^2+3328/49*a-169536/343)*1*z^6+(-166272/2401*a^2+3328/343*a-169536/2401)*z^7
La séptica de Labs
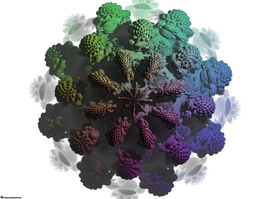
Las Matemáticas son retos / Problema abierto
¿Te imaginas cuál es el máximo número de singularidades que puede llegar a tener una superficie? Dependiendo del grado de la ecuación el número máximo de singularidades que se puede alcanzar es diferente.
Esta figura, “La Séptica de Labs”, fue construida en 2004 por Oliver Labs. Tiene grado siete y es importante porque su número de singularidades, 99, es el más cercano al máximo posible conocido hasta hoy.
En efecto, en 1982 A. N. Varchenko demostró que no se pueden obtener superficies de grado siete con más de 104 singularidades y, hasta ahora, nadie ha llegado más lejos que Labs. Por eso la construcción de sépticas con 100, 101, 102, 103 o 104 singularidades continúa siendo un problema abierto.
Licencia CC BY-NC-SA-3.0
Fórmula
- S_5(x, y)+t(z) = 0\\ S_5(x, y) = x^5−10x^3y^2+5xy^4−5x^4−10x^2y^2− 5y^4+20x^2+20y^2−16\\ t(z) = −3z^5+10z^3−15z−8
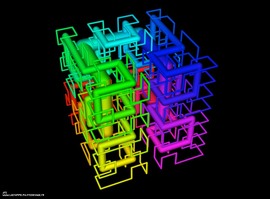
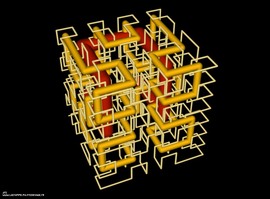
Quintica con 15 cúspides
Esta superficie de grado 5 (quintica) tiene 15 singularidades cuyo tipo se llama cúspide ordinaria o A2. La superficie es parte de una serie de superficies relacionadas de una infinidad de grados construidos por Oliver Labs en 2005. Como puede uno ver en la imagen, cinco de las singularidades se ven diferentes de las otras. Estas cinco son más específicamente del tipo A2++ y las otras del tipo A2+−. La primera puede ser descrita localmente mediante la ecuación x3+y2+z2 = 0, las otras mediante x3+y2−z2 = 0. La ecuación de la quintica con 15 cúspides es S5(x, y)+t(z) = 0, donde S5(x, y) = x5−10x3y2+5xy4−5x4−10x2y2− 5y4+20x2+20y2−16 es un pentágono regular, y donde el polinomio t(z) = −3z5+10z3−15z−8 es una variante de los llamados Polinomios de Chebyshov.
Licencia CC BY-NC-SA-3.0
Quintíca de Togliatti
Ecuación de W. Barth (1995).
Visualización: Oliver Labs
Licencia CC BY-NC-SA-3.0
Cuártico Kummer
Ecuación de E. E. Kummer (1860s).
Visualización: Oliver Labs
Licencia CC BY-NC-SA-3.0
Superficie cúbica con una singularidad D4
Ecuación: Clásica (Siglo XIX), adaptada por Oliver Labs.
Visualización: Oliver Labs
Licencia CC BY-NC-SA-3.0