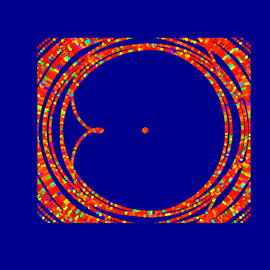
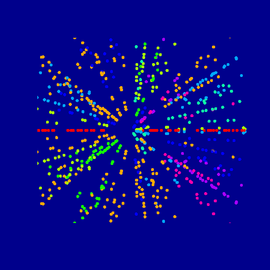
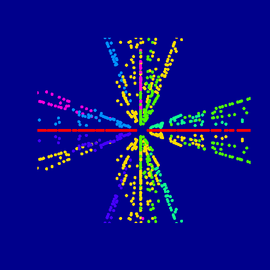
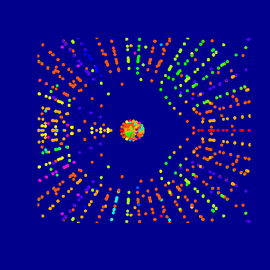
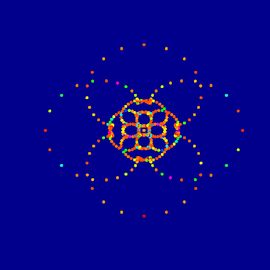
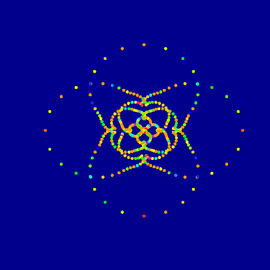
Sunset at the Sea of Primes
The pictures show a colorful visualization of a complex function, whose nulls are located at all primes on the real axis. The formula is shown below.
Links to related videos:
http://youtu.be/pkJ0GoFsBqs
http://youtu.be/trOkyzhb2RY
http://youtu.be/MDx5W4MaIcI

Formula
- f(z) = \left| 2 - \sum\limits^\infty_{k=1} \frac{1}{k} \frac{e^{2 \pi i z}-1}{ e^{2 \pi i z / k}-1} \right|
Sunset at the Sea of Primes

Sunset at the Sea of Primes (detail)


Ray of Primes 2
Primes at the right hand side can be identified by a blue “flame” overtopping the other integers.

Prime Spiral 1
Inspired by Ulam’s prime spiral: the ray of primes warped to an Archimedes spiral.


Prime Spiral 3

Prime Spiral 4
Here, the same distance between numbers and between spiral arms was chosen. This leads to a chaotic distribution of primes.

Prime Spiral 5
Here, the distance between numbers are pi times of the distance between spiral arms. Now primes are forming interesting patterns.


Prime Spiral 7
Here, the distance between numbers are pi/3 times of the distance between spiral arms. Again, primes are forming interesting patterns.

Prime Spiral 8
Here, the distance between numbers are pi/8 times of the distance between spiral arms. Again, primes are forming interesting patterns.
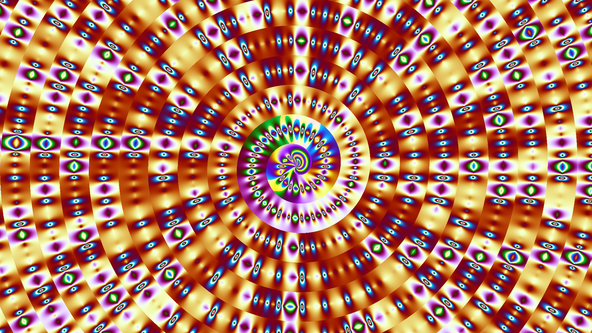

Prime Spiral 10
Here, the distance between numbers are 3.19 times of the distance between spiral arms.