My contributed pictures for the Imaginary / NIMS exhibition at ICM Seoul 2014
Some of my pictures were chosen by the Imaginary team to be displayed at their ICM exhibition in Seoul.
You can view them here, with the associated explanation. Those pictures were only part of the set of displayed pictures by other contributors.

Apophysis
In 1988, Michael Barnsley developped the theory of Iterated Function Systems (IFS in short), a way of describing and generating fractals well suited for programming. The functions used were all affine transforms, and can generate objects like ferns, Sierpinski gaskets… Apophysis (www. aphophysis.org) is a computer program, initiated by Scott Draves, which generalize IFS by using non linear functions instead of affine ones. Apophysis interface is quite complete and user friendly, allowing easy and fast experiments. This program is a good illustration of what experimental mathematics can offer : fast tests, large universe of possibilities.

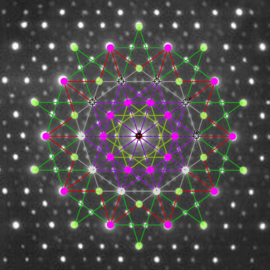
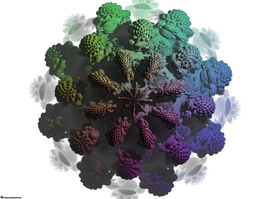
Cardioidal Variation
The cardioid is a very current curve which can be generated in a lot of different ways : rolling a coin around another one, by reflection of sunlight into a milk pan (may be the first encounter with a not simple mathematical object for children) Pedoe method defines it as the envelop of a set of circles.If you rotate those circles in order to produce a 3dimensionnal object, and if you try different ways to control this rotation, you can produce an infinity of very appealing structures, like this one, which inspired british milliner Gabriela Ligenza for creating the first line of 3d printed hat
<a href=”http://archive. bridgesmathart.org/2014/bridges2014-349.pdf “>This paper</a> contains some more explanations and examples.

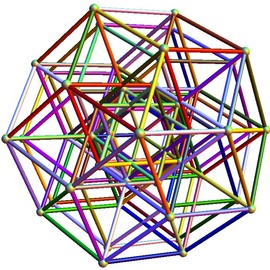
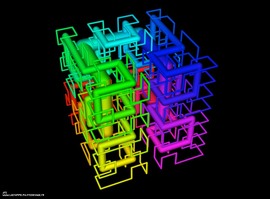
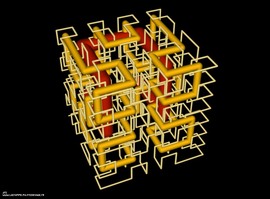
Compound of five quasi hamiltonian circuits on a truncated icosidodecahedron
It is know, that every archimedean solid has an hamiltonian circuit relying al of its vertices.
It is not so easy to find one of those circuits when your are more a computer scientist than a mathematician !
I just succeeded in finding a 104 vertices path on a truncated icosidodecahedron (instead of 120)
i then connected those 104 points with a curved line, and duplicated five time this path, with the same transformations that produces the compound of five tetrahedra from a single initial .
The last trick was to rotate the structure in order to hide the less symetric parts.
Mathematics can be beautiful, even if not perfect.

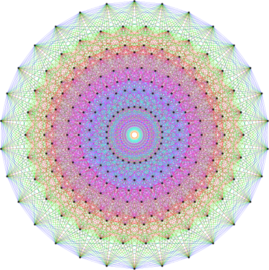
Doyle Spiral
Doyle Spirals are a particular case of circle packing: each circle is surrounded with 6 tangent circles. When the parameters are well chosen (and this is the hard stuff), this circle packing can tile the plane. Applying to this tiling geometric transformations preserving the tangency property, one can create elegant patterns. This work was initiated while looking at the beautiful and challenging images created by Jos Leys.

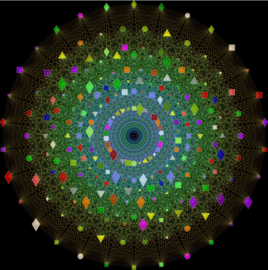
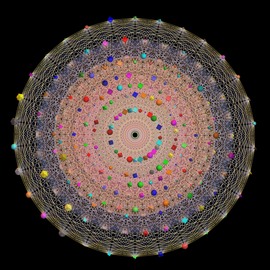
A Whiter Shade of Deep Purple
Circle packing can be seen as the art of placing tangent circles on the plane, leaving as little unoccupied space as possible. The so called Apollonian Gasket recursively fills the space between tangent circles. But this method leaves large empty spaces inside the initial circles. The Steiner Chain method puts a chain of tangent circles between two circles. Here, I combined two methods and applies them repeatedly. Moreover, in order add more exploration possibilities, transforms that preserves circles and tangency are applied : circle inversions and mobius transforms