Jean Constant - Bell numbers
The Bell numbers are named after mathematician and writer Eric Temple Bell. The Bell numbers (1, 1, 2, 5, 15, 52, 203, 877, 4140, 21147, 115975, 678570, 4213597, …) describe the number of ways a set with n elements can be partitioned into disjoint, non-empty subsets.
Wolfram contributor Robert Dickau completed several series of mathematical figures in fractal, chaos and combinatorial problems and among them, a series of diagrams relating to Bell numbers using the proprietary development computational platform, Mathematica
The following are two examples from a 15 image series done after Dickau’s diagrams on Bell numbers and available at hermay.org

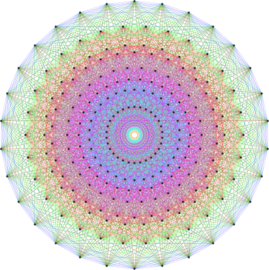
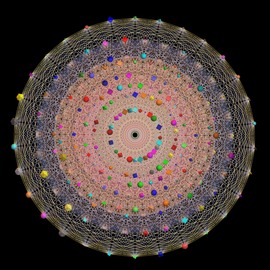
Bell number #1
From R. Dickau’s diagram #5 of the set {1, 2, 3, 4}, 15 partitions.
The line that connects the elements in the same subset were abstracted in various original forms.
The point representing the singleton subset was transformed and assigned a specific visual identity.
The shapes were repositioned in a composition consistent with Dickau’s original demonstration.

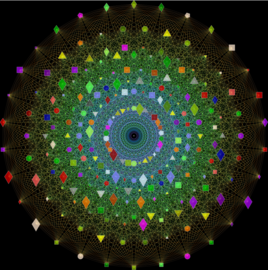
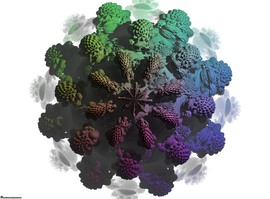
Bell number #2
From R. Dickau Diagram #7 of the set {1, 2, 3, 4}, 15 partitions.
Same process as example #1, set on a different background.
The visual identification of the points representing the singleton subsets was kept the same as the thread between the 15 plates visualization.