Imaginary Chmutov's octics
The original visualizations were created after a loose interpretation of the Chumtov octic equation in the Surfer program. The challenge for a visual artist was to translate the complex 3D surface into a a meaningful 2D statement. The resulting objects were re-processed in various graphic application to recreate a new context inspired by the source geometry. The citrus component - a copy of the Surfer program logo - was added as a reference to the original program and a tribute to the quality and originality of the software.
Singular proposition
Chmutov’s octic equation written by SV Chmutov in the early 80s. At the time, it constituted the world record for μ(d) most d. Beginning numbers have been replaced by some of the Fibonacci numbers sequence. Full description of the process is available on the following page http://www. hermay.org/jconstant/surfer/resource.html
0.19 a, 0.06 z
(a*(-55*34))/21+x^13+y^8+z^5-3*2*x^1-1*2*y^6-1*2*z^6+1.25*x^4+1.25*y^4+1.25*z^4-1*0.25*x^2-1*0.25*y^2-1*0.25*z^2+0.03125

Octic in a a square
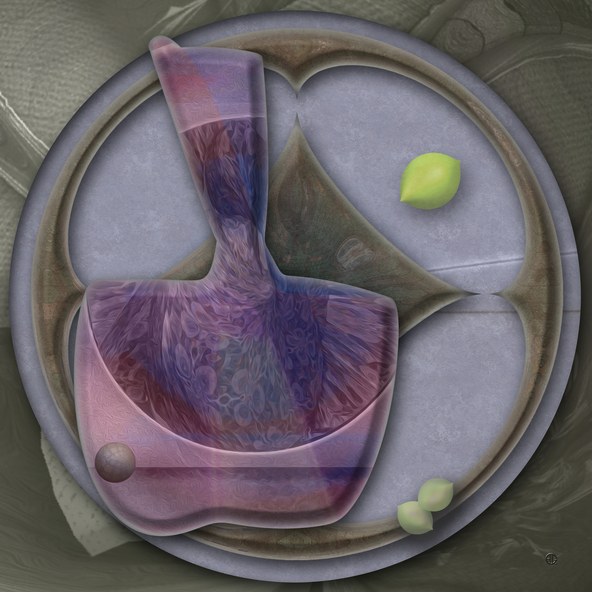
Chmutov octic #2 on a vis a vis background disk. The cusp on the surface is a singularity. Black holes and the Big Bang constitute singularities cosmological model equations. The original equation has been altered with reverse Fibonacci numbers sequence. Full description of the process is available on the following page http://www. hermay.org/jconstant/surfer/resource.html
a) 0.01 z
x^5-x^3+y^2+y^1+z^1-z^0
b) 0.19 a, 0.06 z
(a*(-55*34))/21+x^13+y^8+z^5-3*2*x^1-1*2*y^6-1*2*z^6+1.25*x^4+1.25*y^4+1.25*z^4-1*0.25*x^2-1*0.25*y^2-1*0.25*z^2+0.03125 = 0

The octic's tabernacle
Variation on the Chmutov’s octic equation that brings up its symmetrical aspect. Included, a parabola created in the Surfer program. Full description of the process is available on the following page http://www. hermay.org/jconstant/surfer/resource.html
a) 0.53 z
(a*(-55*34))/21+x^13+y^8+z^5-3*2*x^1-1*2*y^6-1*2*z^6+1.25*x^4+1.25*y^4+1.25*z^4-1*0.25*x^2-1*0.25*y^2-1*0.25*z^2+0.03125 (a*(-55*34))/21+x^13+y^8+z^5-3*2*x^1-1*2*y^6-1*2*z^6+1.25*x^4+1.25*y^4+1.25*z^4-1*0.25*x^2-1*0.25*y^2-1*0.25*z^2+0.03125 = 0
b) 0.41 z
x*y*(x^2-y)




















