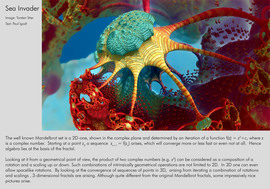
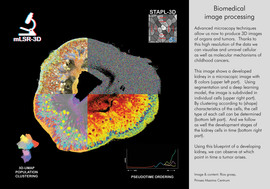
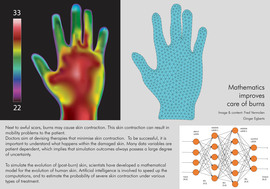
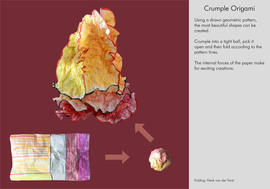
Reaction-diffusion equations
Allen-Cahn equation: describes phase separation of two media.
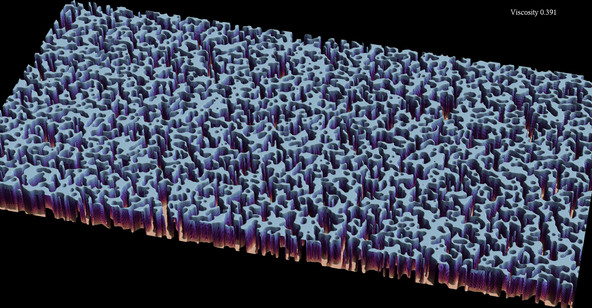
Rock-Paper-Scissors-Lizard-Spock equation: describes 5 competing chemicals
Formül
- \partial_t u = \Delta u + u - u^3
Solution of the 2D Allen-Cahn equation

Formül
- \begin{align} \partial_t u_1 &= \Delta u_1 + u_1(1 - \rho - au_2 - au_4) \\ \partial_t u_2 &= \Delta u_2 + u_2(1 - \rho - au_3 - au_5) \\ \partial_t u_3 &= \Delta u_3 + u_3(1 - \rho - au_4 - au_1) \\ \partial_t u_4 &= \Delta u_4 + u_4(1 - \rho - au_5 - au_2) \\ \partial_t u_5 &= \Delta u_5 + u_5(1 - \rho - au_1 - au_3) \\ \rho &= \sum_{i=1}^5 u_i, a = 0.75 \end{align}
Rock-Paper-Scissors-Lizard-Spock reaction-diffusion equation
Solution of a reaction-diffusion equation with five competing chemicals.

Formül
- \begin{align} \partial_t u_1 &= \Delta u_1 + u_1(1 - \rho - au_2 - b(t)u_4) \\ \partial_t u_2 &= \Delta u_2 + u_2(1 - \rho - au_3 - b(t)u_5) \\ \partial_t u_3 &= \Delta u_3 + u_3(1 - \rho - au_4 - b(t)u_1) \\ \partial_t u_4 &= \Delta u_4 + u_4(1 - \rho - au_5 - b(t)u_2) \\ \partial_t u_5 &= \Delta u_5 + u_5(1 - \rho - au_1 - b(t)u_3) \\ \rho &= \sum_{i=1}^5 u_i, a = 0.75 \end{align}
Asymmetric Rock-Paper-Scissors-Lizard-Spock reaction-diffusion equation

Formül
- \partial_t u = \Delta u + u - u^3
Allen-Cahn equation on the sphere
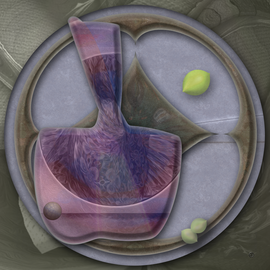
Solution of the Allen-Cahn equation for phase separation on the 2d sphere. The color hue and radial coordinate indicate the value of the field.
Formül
- \begin{align} \partial_t u &= D\Delta u + u(1 - \rho - av) \\ \partial_t v &= D\Delta v + v(1 - \rho - aw) \\ \partial_t w &= D\Delta w + w(1 - \rho - au) \\ \rho &= u + v + w \\ D &= 0.2, a = 0.75 \\ \end{align}
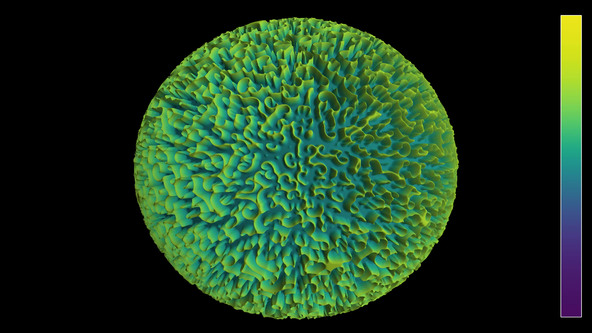
Rock-paper-scissors reaction-diffusion equation on the sphere
Solution of a reaction-diffusion equation with three fields on the sphere. Each species beats one of the others, and is beaten by the other one. The color hue and radial coordinate show the value of the first field.
Formül
- \begin{align} \partial_t u &= D\Delta u + u(1 - \rho - av) \\ \partial_t v &= D\Delta v + v(1 - \rho - aw) \\ \partial_t w &= D\Delta w + w(1 - \rho - au) \\ \rho &= u + v + w \\ D &= 0.2, a = 0.75 \\ \end{align}
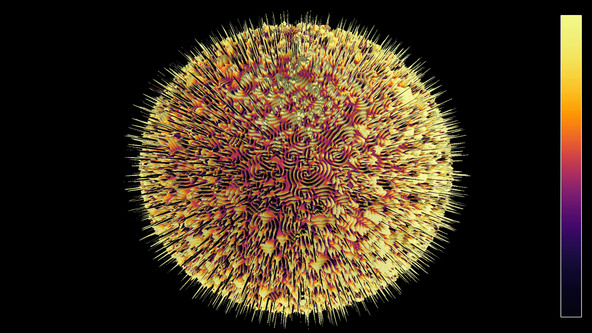
Rock-paper-scissors reaction-diffusion equation on the sphere, vorticity
Solution of a reaction-diffusion equation with three fields on the sphere. Each species beats one of the others, and is beaten by the other one. The color hue and radial coordinate show the vorticity of a phase variable derived from the concentrations.

Formül
- \begin{align} \partial_t u &= D\Delta u + u(1 - \rho - av) \\ \partial_t v &= D\Delta v + v(1 - \rho - aw) \\ \partial_t w &= D\Delta w + w(1 - \rho - au) \\ \rho &= u + v + w \\ D &= 0.2, a = 0.75 \\ \end{align}
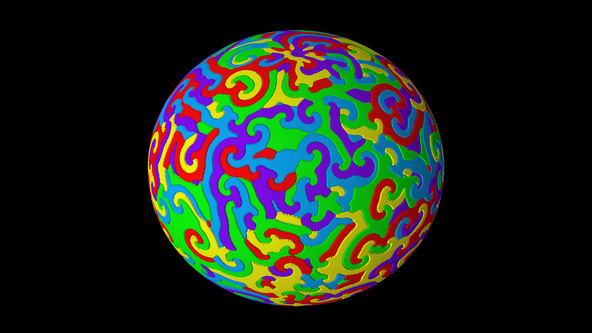
Spirals in the rock-paper-scissors reaction-diffusion equation on the sphere
Solution of a reaction-diffusion equation with three fields on the sphere. Each species beats one of the others, and is beaten by the other one. The color hue and radial coordinate show the vorticity of a phase variable derived from the concentrations.
Formül
- \begin{align} \partial_t u_1 &= \Delta u_1 + u_1(1 - \rho - au_2 - au_4) \\ \partial_t u_2 &= \Delta u_2 + u_2(1 - \rho - au_3 - au_5) \\ \partial_t u_3 &= \Delta u_3 + u_3(1 - \rho - au_4 - au_1) \\ \partial_t u_4 &= \Delta u_4 + u_4(1 - \rho - au_5 - au_2) \\ \partial_t u_5 &= \Delta u_5 + u_5(1 - \rho - au_1 - au_3) \\ \rho &= \sum_{i=1}^5 u_i, a = 0.75 \end{align}
Rock-Paper-Scissors-Lizard-Spock reaction-diffusion equation on the sphere
Solution of a reaction-diffusion equation with five competing chemicals on the sphere.

Formül
- \begin{align} \partial_t u_1 &= \Delta u_1 + u_1(1 - \rho - au_2 - b(t)u_4) \\ \partial_t u_2 &= \Delta u_2 + u_2(1 - \rho - au_3 - b(t)u_5) \\ \partial_t u_3 &= \Delta u_3 + u_3(1 - \rho - au_4 - b(t)u_1) \\ \partial_t u_4 &= \Delta u_4 + u_4(1 - \rho - au_5 - b(t)u_2) \\ \partial_t u_5 &= \Delta u_5 + u_5(1 - \rho - au_1 - b(t)u_3) \\ \rho &= \sum_{i=1}^5 u_i, a = 0.75 \end{align}
Asymmetric Rock-Paper-Scissors-Lizard-Spock reaction-diffusion equation on the sphere
Solution of a reaction-diffusion equation with five competing chemicals on the sphere.

Formül
- \begin{align} \partial_t u_1 &= \Delta u_1 + u_1(1 - \rho - au_2) \\ \partial_t u_2 &= \Delta u_2 + u_2(1 - \rho - au_3) \\ \partial_t u_3 &= \Delta u_3 + u_3(1 - \rho - au_4) \\ \partial_t u_4 &= \Delta u_4 + u_4(1 - \rho - au_5) \\ \partial_t u_5 &= \Delta u_5 + u_5(1 - \rho - au_1) \\ \rho &= \sum_{i=1}^5 u_i, a = 0.75 \end{align}
Asymmetric Rock-Paper-Scissors-Lizard-Spock reaction-diffusion equation on the sphere
Solution of a reaction-diffusion equation with five competing chemicals on the sphere.