The Real Projective Plane
실사영평면(real projective plane)은 2차원의 닫힌 곡면(다양체)입니다. 보통의 유클리드 평면에서 직선들에 대해 무한점을 직선이 향하는 양쪽 방향마다 하나씩 추가합니다. 그러면 모든 평행선들이 한 점에서 만나게 되고, 여기서 (두 선분이 만나지 않는) 평행의 개념이란 존재하지 않습니다. 무한점들의 합집합은 또 다른 직선이 됩니다.
이렇게 만든 공간은 어떻게 생겼을까요?
뫼비우스 띠의 닫힌 곡선 경계를, 원판의 경계에 꿰메는 것을 상상해 보세요…
여기의 그림들은 손으로 그린 보이(Boy)의 첫번째 곡면을 제외하고는 모두 무료 레이 트레이싱 프로그램 POV-Ray(Peristence of Vision Raytracer)로 제작되었습니다.

정신을 구부릴 수 있을까요?
뫼비우스 띠의 곡선 경계를,
원판의 경계에 꿰메는 것을,
생각해 보세요…
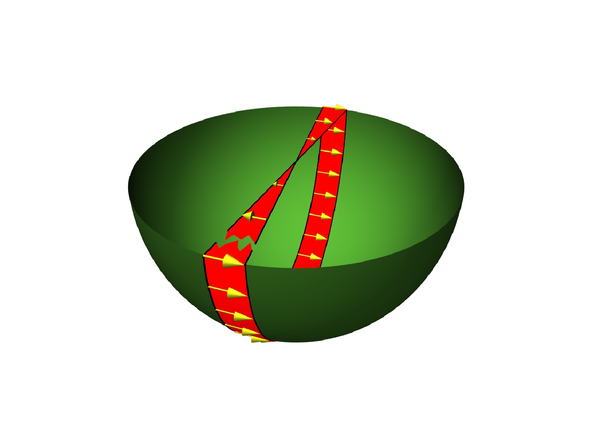
원판은 위상적으로 반구와 동일합니다. 이 그림에 쓰인 뫼비우스 띠는 클라인 병의 아래쪽 절반입니다.

'사영평면'의 이름의 유래?
‘사영평면’이라는 용어를 설명하기 위해 평면 위의 두 평행선을 생각해 봅시다. 철로 위의 두 기찻길이 (비록 평면에 있지는 않지만) 좋은 예가 될 것입니다. 이 둘은 마치 지평선 위에서 만나는 것처럼 보입니다. 이를 계기로 17세기 초의 케플러(Johannes Kepler), 데자르그(Gérard Desargues), 나중에는 퐁슬레(J. V. Poncelet) 들이 독립적으로, 실평면에 평행선이 만나는 점들을 추가한 사영평면을 생각하게 되었습니다.
비가향성(nonorientibility)
반구에서 적도의 서로 반대쪽에 있는 점들을 붙인다면, 이는 사영평면의 모형이 됩니다. 닫힌 평면이 비가향(non-orientable)일 필요충분조건은, 따라갔을 때 방향이 바뀌는 닫힌 곡선인 뫼비우스 곡선(Möbius curve)을 내부에 포함하고 있는 것입니다. 뫼비우스 띠는 이 뫼비우스 곡선의 작은 근방(neighborhood)이 됩니다.
위의 그림은 실사영평면 속의 직선을 따라가며 생성된 뫼비우스 띠를 보여줍니다. 반대되는 점을 붙였으므로 이 직선은 닫힌 곡선이 되고, 방향이 바뀝니다. 따라서 사영평면이 비가향임을 알 수 있습니다.
공식
- \varphi: \mathbb P^2 \rightarrow \mathbb R^3 \,\, with \,\, \varphi := f\mid _{\mathbb P^2} \,\, and \,\, f \,\, as follows:
- f(x,y,z) := \left(xz, yz, \frac{1}{2}(z^2-x^2) \right)
크로스캡(crosscap)
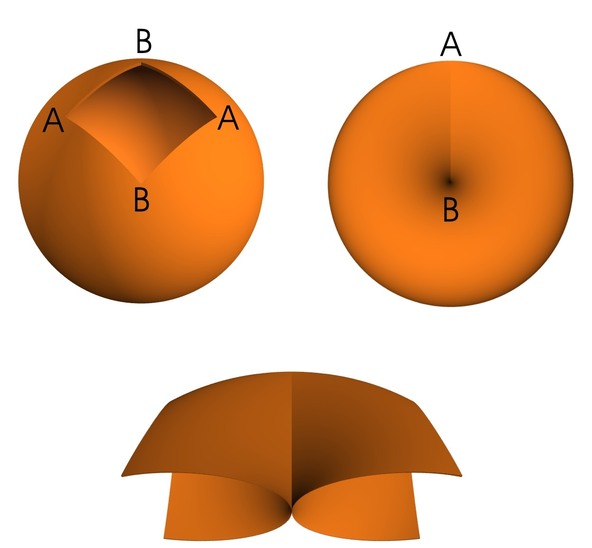
실사영평면의 반구 모형의 가장자리를 한번 이어보겠습니다. 좌상단에서 보이는 것처럼 반구를 변형하는 것을 상상해 보세요. 그 다음 마주보는 변들의 쌍을 꿰매 이들이 자기교차하는 선분이 생기게 합니다. 십자형 연결으로 만들어진 우상단에 보이는 이 모양을 크로스캡(crosscap)이라 부릅니다. 이 이중점들의 선분은 끝점(pinch-point) 혹은 분기점(branch-point)이라 불리는 점 A, B에서 끝납니다. 이 특이점 형태는 Whitney umbrella라 불리고 쌍으로 나타납니다. A점의 근방 모습이 하단 그림에 묘사되어 있습니다.
그림에 영감을 주고 공식을 참고한 출처입니다:
Ulrich Pinkall. Modelle der reellen projektiven Ebene. In Gerd Fischer, editor, Mathematische Modelle, Aus den Sammlungen von Universitäten und Museen (Kommentarband), 페이지 69 – 73, Akademie-Verlag, Berlin, 1986.

공식
- \varphi: \mathbb P^2 \rightarrow \mathbb R^3 \,\, with \,\, \varphi := f\mid _{\mathbb P^2} \,\, and \,\, f \,\, as follows:
- f(x,y,z) := \left(xy, yz, zx \right)
로마 곡면(The Roman Surface)
이 모양은 수학자 스타이너(Jakob Steiner)가 발견하였습니다. 로마 곡면이라는 이름은 그가 로마에 1844년에 체류하면서 기하학적 성질을 연구한 데에서 나온 것입니다. 하지만 이 곡면과 스타이너의 연구가 세상에 알려진 것은 그가 작고한 해인 1863년 그의 친구인 바이어슈트라스(Karl Weierstraß)가 퍼낸 논문에 의해서였습니다.
이 곡면에는 교차로 이루어진 세 선분이 있습니다. 이들은 각각의 이중점(double point)을 가지고, 중간의 일반 삼중점(ordinary triple point)에서 모두 만납니다. 선분들의 끝점들은 Whitney umbrella 특이점 형태를 갖습니다.
그림의 영감을 주고 공식을 참고한 출처입니다:
Ulrich Pinkall. Modelle der reellen projektiven Ebene. In Gerd Fischer, editor, Mathematische Modelle, Aus den Sammlungen von Universitäten und Museen (Kommentarband), pages 69 – 73, Akademie-Verlag, Berlin, 1986.
보이(Boy)의 첫번째 곡면
수학자 힐베르트(David Hilbert)는 사영평면을 3차원 유클리드 공간 속에 부드럽게 넣을(immerse)수 없다고 생각하였습니다. Whitney umberlla 형태의 특이점을 제거할 수 없었기 때문입니다. 하지만 그의 학생 보이(Werner Boy)에게 이를 증명하라는 문제를 주었는데, 보이는 1901년 박사논문에 부드럽게 넣는 방법을 구성해 스승을 놀라게 하였습니다. 그는 평행한 평면으로 곡면을 자른 단면 곡선들로 부드럽게 넣은 곡면을 묘사했습니다. (그의 박사논문에 사용된 왼쪽의 그림을 참고하세요) 오른쪽 부분은 보이의 곡면을 단면 곡선과 함께 공간에 나타낸 모습을 보여줍니다.

공식
- \begin{eqnarray*} 0&=&64\left(1-z\right)^3z^3-48\left(1-z\right)^2z^2\left(3x^2+3y^2+2z^2\right)\cdots\\ &&{}+12\left(1-z\right)z\left[27\left(x^2+y^2\right)^2-24z^2\left(x^2+y^2\right) \right.\cdots\\ &&\left.{}+36\sqrt{2}yz\left(y^2-3x^2\right)+4z^4\right] +\left(9x^2+9y^2-2z^2\right)\cdots\\ &&{}*\left[-81\left(x^2+y^2\right)^2-72z^2\left(x^2+y^2\right)+108\sqrt{2}xz\left(x^2-3y^2\right)+4z^4\right] \end{eqnarray*}
보이(Boy)의 두번째 곡면
보이(Werner Boy)의 첫번째 곡면은 3중 대칭을 갖고 있는 도형으로 변형될 수 있습니다. 이를 이용해 보이는 두 번재 곡면을 만들었고, (박사논문에 사용된) 왼쪽의 그림처럼 높이에 따른 단면으로 이 곡면을 기술했습니다. 오른쪽의 부분은 비슷한 높이에서 곡면을 잘랐을 때의 전체 모양을 보여줍니다.
공식응 참조한 출처:
François Apéry. Models of the real projective plane. Vieweg, Braunschweig / Wiesbaden, 1987.

공식
- \varphi: \mathbb P^2 \rightarrow \mathbb R^3, \,\,p \in \mathbb P^2 \, \, \varphi(p):=(f_1(p),f_2(p),f_3(p))
- \begin{eqnarray*} f_1(x,y,z)&=& \frac{1}{2}\left[\left(2x^2-y^2-z^2\right)\left(x^2+y^2+z^2\right)+2yz\left(y^2-z^2\right)\right.\cdots\\ & & \left.{}+zx\left(x^2-z^2\right)+xy\left(y^2-x^2\right)\right]\\ f_2(x,y,z)&=& \frac{\sqrt{3}}{2}\left[\left(y^2-z^2\right)\left(x^2+y^2+z^2\right)+zx\left(z^2-x^2\right)+xy\left(y^2-x^2\right)\right]\\ f_3(x,y,z)&=& \left(x+y+z\right)\left[\left(x+y+z\right)^3+4\left(y-x\right)\left(z-y\right)\left(x-z\right)\right] \end{eqnarray*}
보이 곡면의 여러 모습
각 열의 그림들은 같은 방향에서 본 곡면들을 나타냅니다. 첫 번째 열은 z축의 음수 방향 (모든 12개 그림에서 x축은 수평으로 놓여집니다)에서 본 모습이고, 다음 열들은 곡면을 x축에 대해 60°, 120°, 180° 돌린 모습입니다.
첫째 행에서는 곡면들이 잘리지 않은 그대로 보여지고, 둘째 행에서는 바라보는 시점에 수직인 평면으로 약간만 들어가서 자른 단면을 보여줍니다. 셋째 행에서는 원점과 x축을 지나가는 평면으로 더 나아가 자른 담녀을 보여줍니다. 12개의 그림에는 모두 같은 방향의 조명 효과가 적용됩니다. 셋째 3행의 처음과 끝 그림은 완전히 반대되는 것으로, 이 둘을 합쳐 닫힌 보이 곡면을 만들 수 있습니다.
공식을 참조한 출처입니다:
François Apéry. Models of the real projective plane. Vieweg, Braunschweig / Wiesbaden, 1987.

삼중 대칭
보이의 두 번째 곡면은 3중 대칭을 갖고 있으므로, 3개의 합동인 조각들로 쪼갤 수 있습니다. 이 그림은 Robert Bryant의 매개화를 사용해서 나온 왼쪽의 곡면을, 같은 조각 3개로 잘라 오른쪽처럼 단면을 보여줍니다. 대칭성에서 아름다움을 느낄 수 있습니다.

3날 프로펠러
보이 곡면은 유클리드 공간의 자기교차(self-transversal)하는 몰입입니다. 따라서 다중점에서 이들의 역상(preimage)에 대응되는 접평면들의 대응을 생각하면 여러 개의 접평면들을 그을 수 있습니다.
자기교차 곡면의 삼중점들은 고립되어 있고, 이중점은 닫혀 있거나 무한대로 뻗어 나가는 곡선들이, 경계에서 종료되거나 Whitney umbrella 특이점에서 끝날 때 생성됩니다.
이 그림은 보이의 두번째 곡면의 자기교차 하는 부분의 곡선의 근방을 나타냅니다. 마치 3개의 날이 달린 프로펠러처럼 생겼습니다. 색깔들은 곡면의 교차하는 다른 면들을 잘 구별하기 위해 칠해졌지만, 이들은 물론 같은 곡면 위에 있습니다.
변형
Bernard Morin은 3쌍 6개의 Whitney umbrella 특이점들을 제거함으로서 로마 곡면을 보이 곡면으로 변형하는 방법을 처음 생각해냈습니다. François Apéry가 정확한 호모토피(homotopy) 변형을 구성했습니다. 삼중점과 3중대칭의 축은 변형에서 계속 보존됩니다. 그림에서는 로마 곡면(원색 파란색)에서 보이 곡면(원색 빨간색)으로의 변형 중 15개의 중간단계가 묘사됩니다.