Stepan Tersian, Gallery I
이 갤러리 I에는 8개의 사진과 7개의 그림들이 있습니다. 저는 산티아고 데 콤포스텔라 대학(University of Santiago de Compostela)의 수학과를 방문하면서 갤러리에 대한 영감을 얻었습니다. 산티아고에서의 IMAGINARY 전시는 매우 인상깊었습니다.
저는 수학 소프트웨어 Mathematica와 Maple을 이용해 곡면을 이용한 4개의 작품을 만들었고, 이와 더불어 곡선의 그래프들과 두 수학문제들로 갤러리를 완성하였습니다. 산티아고 데 콤포스텔라, 라 코루냐(A Coruna, 역주: 스페인 갈리시아의 도시), 바이오나(Baiona, 역주: 스페인 갈리시아의 도시), 트랴브나(Tryavna, 역주: 불가리아의 마을) 등에서 촬영한 수학적 내용이 있는 8개의 사진들도 전시됩니다.

The tree of sciences at University of Santiago de Compostela

Atlas with Sphere, Toral square, Santiago de Compostela
이 아틀라스(Atlas, 역주: 그리스 신화의 거인) 석상은, 산티아고 데 콤포스텔라의 사적지 안의 토우랄(Toural) 광장에 있는 벤다냐 대저택(Pazo Bendaña)에 있는 것입니다. 아틀라스는 어깨에 태양과 별들로 장식된 구체를 이고 있습니다. 에우헤니오 그라네이(Eugenio Granell) 재단 및 박물관은 1995년부터 벤다냐 대저택에 자리잡고 있습니다. 초현실주의 예술가인 에우헤니오 그라네이(1912-2001)는 라 코루냐에서 태어나서 유년기와 청년기를 산티아고 데 콤포스텔라에서 보냈습니다.

On the tower of Hercules, A Coruna

Triple helix spiral staircase in the Museum do Pobo Galego
산티아고 데 콤포스텔라에 있는 갈리시아 시민 박물관(Museo do Pobo Galego)의, 3중 나선 구조로 된 특이한 나선 계단입니다.

Spiral staircase 2

Perspective, Baiona

May Sun wood carved ceiling , Daskalov house 1808, Tryavna, Bulgaria
이 특이한 목조 박물관은 트랴브나 마을의 Hristo Daskalov의 옛 집에 있습니다. 상인 Daskalov는 1804년부터 1808년까지 이 박물관을 지었습니다. 두 개의 방의 천장에 새겨진 두 개의 태양은 박물관에서 가장 유명한 전시물입니다. 이 전시물은 장인 Dimitar Oshanesta와 그의 제자 Ivan Bochukovesta가 1808년에 6개월 동안 만들었습니다. 그 둘은 누가 목조 장식으로 천장을 더 아름답게 꾸밀 수 있나 경쟁했습니다. 조각의 형태는 포근한 5월의 태양과 작열하는 7월의 태양을 나타냅니다.

July Sun wood carved ceiling , Daskalov house 1808, Tryavna, Bulgaria

Fruits 1
컵: x2+y2=16z4
사과: (x2+y2+z2)2= x2+y2
레몬: x2+z2=4y3(1-y)3 , 소프트웨어 Maple로 제작.

Lemons and Figs 1
곡면들의 방정식:
x2+y2=4z3(1-z)2 및 x2+y2=64z4(1+z)3,
프로그램 Mathematica로 제작, ParametricPlot3D 함수 이용.

Fruits 2
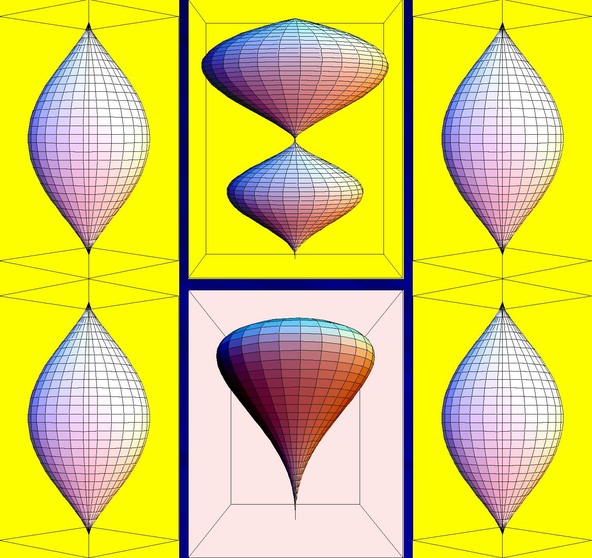
Lemons and Figs 2
곡면들의 방정식:
x2+y2=4z3(1-z)3 (레몬),
x2+y2=4z5(1-z) (무화과) 및 x2+y2=4z2(1-z)5,
프로그램 Mathematica로 제작, ParametricPlot3D 함수 이용.

Circles and ellipses
반지름 r=1.6의 8개 원, CK: {Cos[2πk/n]+r Cos[t], Sin[2πk/n]+r Sin[t]},
{t,0,2π}, k=1,…, 8, n=8.
장축과 단축이 각각 a=1.6, b=1.2인 8개 타원, {t,0,2 π}, k=1,…, 8, n=8.
E_K:{Cos[2πk/n]+a Cos[2πk/n] Cos[t] +b Sin[2πk/n] Sin[t],
Sin[2πk/n] - a Sin[2πk/n] Cos[t] +b Cos[2πk/n] Sin[t]}.

Two problems
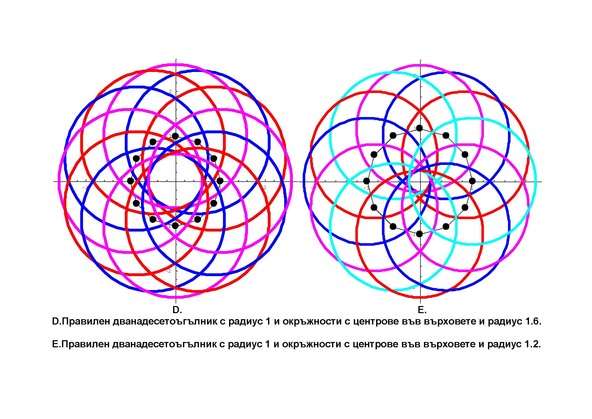
Circles
반지름이 1.2인 12개의 원들, 3가지(왼쪽) 및 4가지(오른쪽) 색깔로 칠해짐
Ck: {Cos[2πk/n]+r Cos[t], Sin[2πk/n]+r Sin[t]}, {t,0,2 π},
k=1,…, 12, n=12.