The National Institute for Mathematical Sciences (NIMS) presents a very special NIMS-IMAGINARY exhibition in collaboration with the ICM committee and the Mathematisches Forschungsinstitut Oberwolfach (MFO). It will feature the best of all IMAGINARY modules of the last years and a lot of new software, images, films and sculptures. It will be the biggest IMAGINARY exhibition shown so far.
TsunaMath
program
Licenses
Source code
Emeği Geçenler
Raouf Hamouda, Emmanuel Audusse, Jacques Sainte-Marie (Developers). Project Numerical Analysis for Geophysics and Environment (Organisation). Institutional support by CEREMA - Compiegne Research Center, UPMC - University Pierre et Marie Curie (Paris), INRIA - Rocquencourt Research Center, France.
Web sitesi
Katkıda Bulunanlar
Tsunamis are big oceanic waves that collide violently with the coast. Most often, tsunamis are created by earthquakes that produce a sudden change on the topography of the ocean seabed. This exhibit explains how tsunamis are modeled mathematically, and recreates simulations of historical catastrophes.
The relationship between the height of the tsunami wave and the magnitude of the seism that causes it is complex. The speed, acceleration, displacement and size of the tectonic plates affect the height of the wave and its initial velocity. Once the wave is traveling across the ocean, the depth of the sea influences also the height and velocity of the water, and once the wave hits
the coast, the slope and the topography of the seabed and coastline modify significantly the wave.
Mathematically, the variables to be calculated are the height of the wave (water depth), and the velocity of the water at each point of the map. The data to be known beforehand is the height of the seabed at each point (bathymetry) and the local modification of this seabed due to the seism. The so called Saint-Venant equations, or shallow water equations, are a set of partial differential equations that model the relations between these variables and data. These equations cannot be solved explicitly, but numerical algorithms can give accurate approximations that allow to obtain good simulations of the wave of a tsunami.
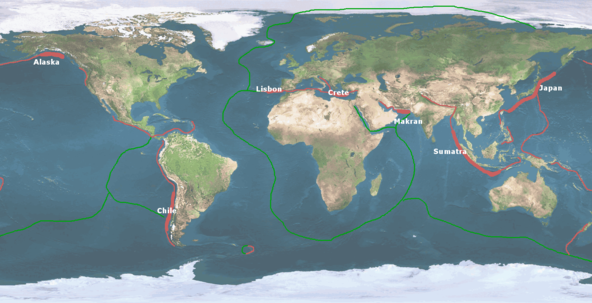
Using these methods, the exhibit shows simulations of great historical tsunamis, such as the Crete tsunami of 365 AD, the Lisbon tsunami of 1755, the Sumatra tsunami of 2004 or the Japan tsunami of 2011. These reconstructions are based on historical documents and descriptions or, in the more recent cases, can be checked against experimental observations to evaluate the validity of the model. Although earthquakes and tsunamis are difficult to predict, these simulations, together with measurements of active seismic zones, can help to reduce the potential impact of tsunamis on populated areas. Building realistic scenarios of affected areas can be used to plan infrastructures accordingly.