Jean Constant - Sangaku
”Wasan” geometry or traditional Japanese mathematics flourished under the Tokugawa shogunate around the Edo period and expressed itself in a unique way through mathematical votive pictures called San Gaku, written in formal Sino-Japanese language and displayed in local temples and public places.
The following two visualizations have been selected from a series of 20 Sangaku problems illustrated by the author and available at hermay.org
A detailed descriptive of the process is available in print at IGI Global Publishing

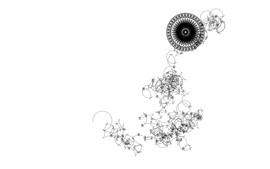
Sangaku problem #1
Problem: If CB’A is an isosceles triangle with CB’ = CA, and B is a point lying on the line B’A, then one of the circles touching the circumcircle of BCB’ internally and also touching AB and AC is twice the size of the incircle of ABC. (H. Okumura, M. Watanabe)
The Klein bottle wireframe reflection was added to emphasize the 3D dynamic of the illustration.

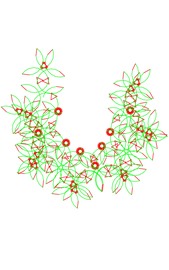
Sangaku problem #2
Problem: in a square PQRS, there are two circles touching SP and the incircle of the square, where one of which touches PQ and the other touches RS. Let A be the point of tangency of QR and the incircle and let the tangents of the two small circles through A intersect the segment SP at B and C. Given the inradius of the square, find the inradius of the circle in the triangle ABC. (H. Okumura.)