Polyhedral Realizations of Flat Tori
A polyhedral surface is obtained by gluing a family of Euclidean polygons along their edges under the condition that glued edges have the same length.
A flat torus is a polyhedral surface without singularity obtained by gluing the opposite sides of a parallelogram.
While it is easy to give a polyhedral realization of a right cylinder, it seems much more difficult to think of such a realization for a given flat torus.
In this gallery, we give PL isometric embeddings of various flat tori by making effective a general method due to Burago and Zalgaller to embed any polyhedral surface. The building block of the construction is a procedure which allows to pleat in a PL and isometric way a big acute triangle above a smaller acute one. It remains to compute an acute triangulation and a short, smooth and conformal embedding of the flat torus we want to embed in order to apply the previous building block.
The pictures were computed thanks to the CGAL library.
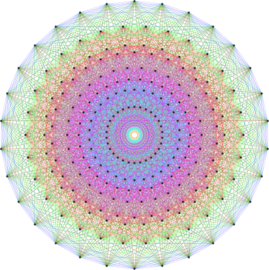
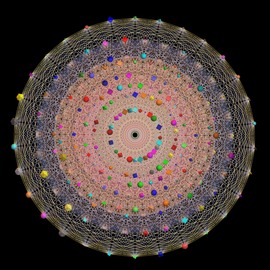
A PL isometric embedding of the square flat torus
A PL isometric embedding of the square flat torus with 170,040 triangles. Each big triangle is pleated inside the initial short embedding to stretch the metric of the initial short embedding.
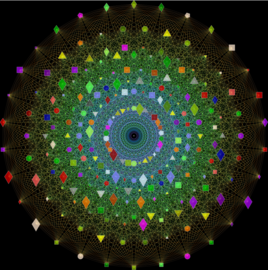
A PL isometric embedding of the square flat torus
A PL isometric embedding of the square flat torus with 170,040 triangles. Each big triangle is pleated inside the initial short embedding to stretch the metric of the initial short embedding.
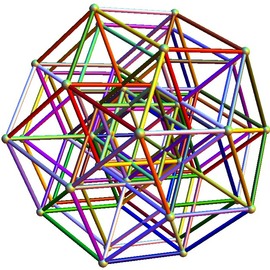
A PL isometric embedding of the square flat torus
A PL isometric embedding of the square flat torus with 170,040 triangles. Each big triangle is pleated inside the initial short embedding to stretch the metric of the initial short embedding.
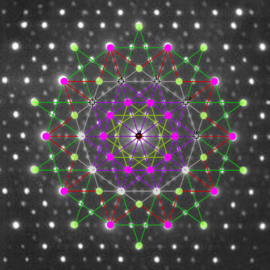
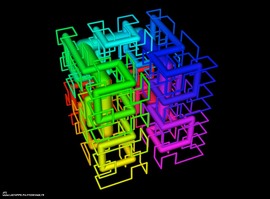
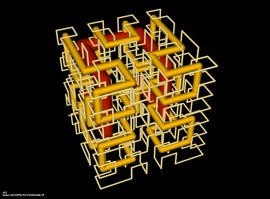
Another PL isometric embedding of the square flat torus
Another PL isometric embedding of the square flat torus with 438,224 triangles. Each big triangle is pleated outside the initial short embedding to stretch the metric of the initial short embedding.
Another PL isometric embedding of the square flat torus
Another PL isometric embedding of the square flat torus with 438,224 triangles. Each big triangle is pleated outside the initial short embedding to stretch the metric of the initial short embedding.
Another PL isometric embedding of the square flat torus
Another PL isometric embedding of the square flat torus with 438,224 triangles. Each big triangle is pleated outside the initial short embedding to stretch the metric of the initial short embedding.
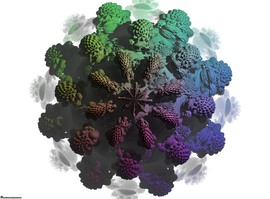
A PL isometric immersion of the hexagonal flat torus
A PL isometric immersion of the hexagonal torus with 7,701,156 triangles. While the triangulation contains almost 8 millions triangles, there remains self-intersections. One should refine the associated triangulation of the torus to obtain an embedding.
A PL isometric immersion of the hexagonal flat torus
A PL isometric immersion of the hexagonal torus with 7,701,156 triangles. While the triangulation contains almost 8 millions triangles, there remains self-intersections. One should refine the associated triangulation of the torus to obtain an embedding.
A PL isometric immersion of the hexagonal flat torus
A PL isometric immersion of the hexagonal torus with 7,701,156 triangles. While the triangulation contains almost 8 millions triangles, there remains self-intersections. One should refine the associated triangulation of the torus to obtain an embedding.
A PL isometric embedding of the rectangular flat torus with modulus (0, 3/2)
A PL isometric embedding of the rectangular torus with modulus (0, 3/2) and 80,400 triangles.
A PL isometric embedding of the rectangular flat torus with modulus (0, 3/2)
A PL isometric embedding of the rectangular torus with modulus (0, 3/2) and 80,400 triangles.
A PL isometric embedding of the rectangular flat torus with modulus (0, 7)
A PL isometric embedding of the rectangular torus with modulus (0, 7) and 1,234,080 triangles.
A PL isometric embedding of the rectangular flat torus with modulus (0, 7)
A PL isometric embedding of the rectangular torus with modulus (0, 7) and 1,234,080 triangles.
A PL isometric embedding of the rectangular flat torus with modulus (0, 7)
A PL isometric embedding of the rectangular torus with modulus (0, 7) and 1,234,080 triangles.
A PL isometric embedding of the flat torus with modulus (1/2, 1/2)
A PL isometric embedding of the torus with modulus (1/2, 1/2) and 139,512 triangles.
A PL isometric embedding of the flat torus with modulus (1/2, 1/2)
A PL isometric embedding of the torus with modulus (1/2, 1/2) and 139,512 triangles.
A PL isometric embedding of the flat torus with modulus (1/2, 1/2)
A PL isometric embedding of the torus with modulus (1/2, 1/2) and 139,512 triangles.